【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
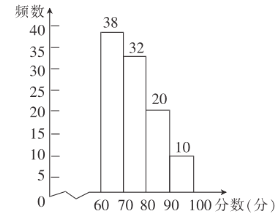
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.
参考答案:
【答案】(1)见解析;(2)见解析;(3)300幅.
【解析】
(1)由60≤x<70频数和频率求得总数,根据频率=频数÷总数求得频数或频率即可;
(2)根据(1)中所求数据补全图形即可得;
(3)总数乘以80分以上的频率即可.
(1)如下表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
| 32 | 0.32 |
| 20 | 0.2 |
| 10 | 0.1 |
合计 | 100 | 1 |
(2)如图.
书法作品比赛成绩频数直方图
(3)![]() 幅,所以全市获得等级奖的幅数为300幅.
幅,所以全市获得等级奖的幅数为300幅.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一批圆心角为90o,半径为3的扇形下脚料,现利用这批材料截取尽可能大的正方形材料,如图有两种截取方法:
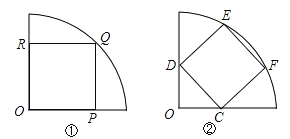
方法一:如图1所示,正方形OPQR的顶点P、Q、R均在扇形的边界上;
方法二:如图2所示,正方形顶点C、D、E、F均在扇形边界上.
试分别求这两种截取方法得到的正方形面积,并说明哪种截取方法得到的正方形面积更大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.

求证:(1)AE=DB;
(2)△CMN为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 的坐标为(0,4),线段
的坐标为(0,4),线段 的位置如图所示,其中点
的位置如图所示,其中点 的坐标为(
的坐标为( ,
,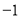 ),点
),点 的坐标为(3,
的坐标为(3, ).
).
(1)将线段
 平移得到线段
平移得到线段 ,其中点
,其中点 的对应点为
的对应点为 ,点
,点 的对应点为点
的对应点为点 .
.①点
 平移到点
平移到点 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;②点
 的坐标为 .
的坐标为 .(2)在(1)的条件下,若点
 的坐标为(4,0),连接
的坐标为(4,0),连接 ,画出图形并求
,画出图形并求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,BC=
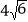 ,则PE+PF的长是( )
,则PE+PF的长是( )
A.
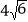 B. 6C.
B. 6C. 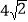 D.
D. 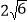
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°;
①求∠OCE的度数. ②若⊙O的半径为
 ,求线段CF的长.
,求线段CF的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

相关试题

