【题目】如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,BC=![]() ,则PE+PF的长是( )
,则PE+PF的长是( )

A. ![]() B. 6C.
B. 6C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
根据三角形的面积判断出PE+PF的长等于AC的长,这样就变成了求AC的长;在Rt△ACD和Rt△ABC中,利用勾股定理表示出AC,解方程就可以得到AD的长,再利用勾股定理就可以求出AC的长,也就是PE+PF的长.
∵△DCB为等腰三角形,PE⊥AB,PF⊥CD,AC⊥BD,
∴S△BCD=![]() BDPE+
BDPE+![]() CDPF=
CDPF=![]() BDAC,
BDAC,
∴PE+PF=AC,
设AD=x,BD=CD=3x,AB=4x,
∵AC2=CD2-AD2=(3x)2-x2=8x2,
∵AC2=BC2-AB2=(![]() )2-(4x)2,
)2-(4x)2,
∴x=2,
∴AC=4![]() ,
,
∴PE+PF=4![]() .
.
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.

求证:(1)AE=DB;
(2)△CMN为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 的坐标为(0,4),线段
的坐标为(0,4),线段 的位置如图所示,其中点
的位置如图所示,其中点 的坐标为(
的坐标为( ,
,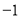 ),点
),点 的坐标为(3,
的坐标为(3, ).
).
(1)将线段
 平移得到线段
平移得到线段 ,其中点
,其中点 的对应点为
的对应点为 ,点
,点 的对应点为点
的对应点为点 .
.①点
 平移到点
平移到点 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;②点
 的坐标为 .
的坐标为 .(2)在(1)的条件下,若点
 的坐标为(4,0),连接
的坐标为(4,0),连接 ,画出图形并求
,画出图形并求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为
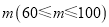 ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.分数段
频数
百分比

38
0.38

0.32


10
0.1
合计
100
1
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°;
①求∠OCE的度数. ②若⊙O的半径为
 ,求线段CF的长.
,求线段CF的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为1的等边三角形,过点C的直线m平行AB,D、E分别是线段AB、直线m上的点,先按如图方式进行折叠,点A、C分别落在A′、C′处,且A′C′经过点B,DE为折痕,当C′E⊥m时,
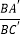 的值为_____.
的值为_____.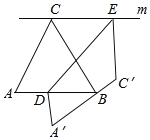
相关试题

