【题目】列一元一次方程解应用问题:
一个蓄水池装有甲、乙两个进水管和丙一个出水管,单独开放甲管3小时可注满一池水,单独开放乙管6小时可注满一池水,单独开放丙管4小时可放尽一池水.
(1)若同时开放甲、乙、丙三个水管,几小时可注满水池?
(2)若甲管先开放1小时,而后同时开放乙、丙两个水管,则共需几小时可注满水池?
(3)若甲管先开放1小时后关闭,而后同时开放乙、丙两个水管,能注满水池吗?并说明理由.
参考答案:
【答案】(1)三个水管同时开放4小时可注满水池;(2)甲管先开放1小时,而后同时开放乙、丙两个水管,则共需![]() 小时可注满水池;(3)先开放甲管1小时后,再开放乙、丙两管不能注满水池.
小时可注满水池;(3)先开放甲管1小时后,再开放乙、丙两管不能注满水池.
【解析】
(1)设三个水管同时开放x小时可注满水池,根据“甲、乙注水量-丙出水量=1”列出方程并解答;
(2)设共需y小时可注满水池,根据“甲、乙注水量-丙出水量=1”列出方程并解答;
(3)设开放甲管1小时后后关闭,再开放乙、丙两管,需z小时可注满水池,根据“甲、乙注水量-丙出水量=1”列出方程并解答.
(1)设三个水管同时开放x小时可注满水池,
根据题意得(![]() +
+![]() )x﹣
)x﹣![]() =1,
=1,
解得x=4,
所以三个水管同时开放4小时可注满水池;
(2)设共需y小时可注满水池,
依题意得![]() +
+![]() ﹣
﹣![]() =1,
=1,
解得y=![]() ,
,
所以若甲管先开放1小时,而后同时开放乙、丙两个水管,则共需![]() 小时可注满水池;
小时可注满水池;
(3)设开放甲管1小时后后关闭,再开放乙、丙两管,需z小时可注满水池,
根据题意得![]() +
+![]() ﹣
﹣![]() =1
=1
解得z=﹣8,
因为﹣8<0不符合实际意义,
所以开放甲管1小时后关闭,再开放乙、丙两管不能注满水池.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正比例函数
 与反比例函数
与反比例函数 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为 其中
其中 .
. 四边形ABCD的是______
四边形ABCD的是______ 填写四边形ABCD的形状
填写四边形ABCD的形状
 当点A的坐标为
当点A的坐标为 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值. 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在
 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 .
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 . 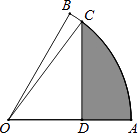
-
科目: 来源: 题型:
查看答案和解析>>【题目】采摘茶叶是茶农一项很繁重的劳动,利用单人便携式采茶机能大大提高生产效率.实践证明,一台采茶机每天可采茶60公斤,是人手工采摘的5倍,购买一台采茶机需2400元.茶园雇人采摘茶叶,按每采摘1公斤茶叶m元的标准支付雇工工资,一个雇工手工采摘茶叶20天获得的全部工钱正好购买一台采茶机.
(1)求m的值;
(2)有两家茶叶种植户王家和顾家均雇人采摘茶叶,王家雇用的人数是顾家的2倍.王家所雇的人中有
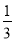 的人自带采茶机采摘,
的人自带采茶机采摘, 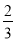 的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶?
的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为
 BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
A. 点E B. 点F C. 点M D. 点N
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, ,
, 都是正三角形,边长分别为2,
都是正三角形,边长分别为2, ,
, ,
, ,且BO,
,且BO, ,
, ,
, 都在x轴上,点A,
都在x轴上,点A, ,
, ,
, 从左至右依次排列在x轴上方,若点
从左至右依次排列在x轴上方,若点 是BO中点,点
是BO中点,点 是
是 中点,
中点, ,且B为
,且B为 ,则点
,则点 的坐标是
的坐标是


A.
 B.
B.  C.
C.  D.
D. 
相关试题

