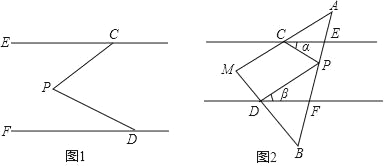
【题目】(问题探究)如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;
(问题迁移)
如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.
(1)当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC= °.
(2)如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC与α、β之间的数量关系,并说明理由.
参考答案:
【答案】【问题探究】∠DPC=α+β,理由详见解析;【问题迁移】(1)70;(2)∠DPC=β﹣α
【解析】
问题探究:延长CP交DF于A,根据平行线的性质以及三角形外角性质进行计算即可;
问题迁移:(1)延长CP交DF于G,根据平行线的性质以及三角形外角性质进行计算即可;
(2)分两种情况进行讨论:点P在BF上,点P在AE上,分别根据平行线的性质以及三角形外角性质进行计算即可.
问题探究:∠DPC=α+β.
理由:如图,延长CP交DF于A,
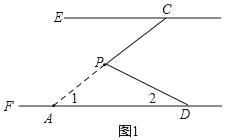
∵DF∥CE,
∴∠PCE=∠1=α,
∵∠DPC=∠2+∠1=180°﹣∠APD,
∴∠DPC=∠2+∠PCE=α+β;
问题迁移:(1)如图2,延长CP交DF于G,
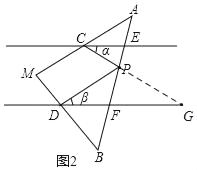
∵DF∥CE,
∴∠PCE=∠G=30°,
∴∠DPC=∠G+∠GDP=30°+40°=70°,
故答案为:70;
(2)如图,∠DPC=β﹣α
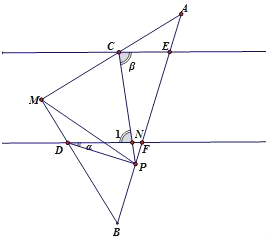
∵DF∥CE,
∴∠PCE=∠1=β,
∵∠DPC=∠1﹣∠FDP=∠1﹣α.
∴∠DPC=β﹣α;
如图,∠DPC=α﹣β
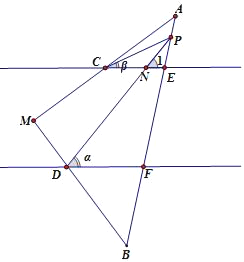
∵DF∥CE,
∴∠PDF=∠1=α,
∵∠DPC=∠1﹣∠ACE=∠1﹣β.
∴∠DPC=α﹣β.
-
科目: 来源: 题型:
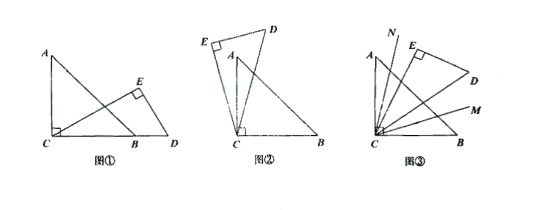
查看答案和解析>>【题目】如图,将一个直角三角板中30°的锐角顶点与另一个直角三角板的直角顶点叠放一起.(注:∠ACB与∠DEC是直角,∠A=45°,∠DEC=30°).
(1)如图①,若点C、B、D在一条直线上,求∠ACE的度数;
(2)如图②,将直角三角板CDE绕点c逆时针方向转动到某个位置,若恰好平分∠DCE,求∠BCD的度数;
(3)如图③若∠DEC始终在∠ACB的内部,分别作射线CM平分∠BCD,射线CN平分∠ACE.如果三角板DCE在∠ACB内绕点C任意转动,∠MCN的度数是否发生变化?如果不变,求出它的度数,如果变化,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(x+y)2+(x﹣y)(2x+y)﹣3x2
(2)

(3)
 .
. (4)y2(y+4)﹣1(y﹣4)﹣1+2(4﹣y)﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=
 (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )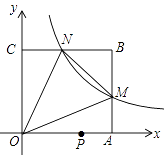
A.6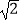
B.10
C.2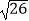
D.2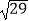
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮一家到桃林口水库游玩.在岸边码头P处,小亮和爸爸租船到库区游玩,妈妈在岸边码头P处观看小亮与爸爸在水面划船,小船从P处出发,沿北偏东60°方向划行,划行速度是20米/分钟,划行10分钟后到A处,接着向正南方向划行一段时间到B处,在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米?(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
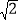 ≈1.41,
≈1.41,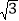 ≈1.73)
≈1.73)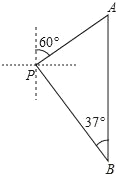
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC=
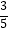 ,则ABCD的面积是 .
,则ABCD的面积是 . 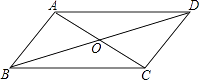
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,如果点P坐标为(m,n),向量
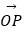 可以用点P的坐标表示为
可以用点P的坐标表示为 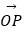 =(m,n).
=(m,n).
已知: =(x1 , y1),
=(x1 , y1),  =(x2 , y2),如果x1x2+y1y2=0,那么
=(x2 , y2),如果x1x2+y1y2=0,那么  与
与  互相垂直,下列四组向量:
互相垂直,下列四组向量:
① =(2,1),
=(2,1), 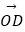 =(﹣1,2);
=(﹣1,2);
② =(cos30°,tan45°),
=(cos30°,tan45°), 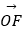 =(1,sin60°);
=(1,sin60°);
③ =(
=(  ﹣
﹣ 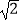 ,﹣2),
,﹣2),  =(
=(  +
+ 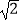 ,
,  );
);
④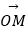 =(π0 , 2),
=(π0 , 2), 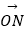 =(2,﹣1).
=(2,﹣1).
其中互相垂直的是(填上所有正确答案的符号).
相关试题

