【题目】如图,在平面直角坐标系xOy中,直线y= ![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣ ![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.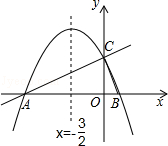
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:①y= ![]() 当x=0时,y=2,当y=0时,x=﹣4,
当x=0时,y=2,当y=0时,x=﹣4,
∴C(0,2),A(﹣4,0),
由抛物线的对称性可知:点A与点B关于x=﹣ ![]() 对称,
对称,
∴点B的坐标为1,0).
②∵抛物线y=ax2+bx+c过A(﹣4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x﹣1),
又∵抛物线过点C(0,2),
∴2=﹣4a
∴a= ![]()
∴y= ![]() x2
x2 ![]() x+2.
x+2.
(2)
解:设P(m, ![]() m2
m2 ![]() m+2).
m+2).
过点P作PQ⊥x轴交AC于点Q,
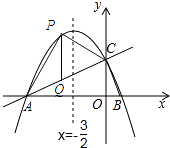
∴Q(m, ![]() m+2),
m+2),
∴PQ= ![]() m2
m2 ![]() m+2﹣(
m+2﹣( ![]() m+2)
m+2)
= ![]() m2﹣2m,
m2﹣2m,
∵S△PAC= ![]() ×PQ×4,
×PQ×4,
=2PQ=﹣m2﹣4m=﹣(m+2)2+4,
∴当m=﹣2时,△PAC的面积有最大值是4,
此时P(﹣2,3).
(3)
解:方法一:
在Rt△AOC中,tan∠CAO= ![]() 在Rt△BOC中,tan∠BCO=
在Rt△BOC中,tan∠BCO= ![]() ,
,
∴∠CAO=∠BCO,
∵∠BCO+∠OBC=90°,
∴∠CAO+∠OBC=90°,
∴∠ACB=90°,
∴△ABC∽△ACO∽△CBO,
如下图:
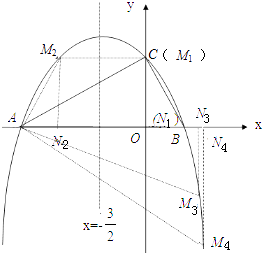
①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;
②根据抛物线的对称性,当M(﹣3,2)时,△MAN∽△ABC;
③当点M在第四象限时,设M(n, ![]() n2
n2 ![]() n+2),则N(n,0)
n+2),则N(n,0)
∴MN= ![]() n2+
n2+ ![]() n﹣2,AN=n+4
n﹣2,AN=n+4
当 ![]() 时,MN=
时,MN= ![]() AN,即
AN,即 ![]() n2+
n2+ ![]() n﹣2=
n﹣2= ![]() (n+4)
(n+4)
整理得:n2+2n﹣8=0
解得:n1=﹣4(舍),n2=2
∴M(2,﹣3);
当 ![]() 时,MN=2AN,即
时,MN=2AN,即 ![]() n2+
n2+ ![]() n﹣2=2(n+4),
n﹣2=2(n+4),
整理得:n2﹣n﹣20=0
解得:n1=﹣4(舍),n2=5,
∴M(5,﹣18).
综上所述:存在M1(0,2),M2(﹣3,2),M3(2,﹣3),M4(5,﹣18),使得以点A、M、N为顶点的三角形与△ABC相似.
方法二:
∵A(﹣4,0),B(1,0),C(0,2),
∴KAC×KBC=﹣1,
∴AC⊥BC,MN⊥x轴,
若以点A、M、N为顶点的三角形与△ABC相似,
则 ![]() ,
, ![]() ,
,
设M(2t,﹣2t2﹣3t+2),
∴N(2t,0),
①| ![]() |=
|= ![]() ,
,
∴| ![]() |=
|= ![]() ,
,
∴2t1=0,2t2=2,
②| ![]() |=
|= ![]() ,
,
∴| ![]() |=2,∴2t1=5,2t2=﹣3,
|=2,∴2t1=5,2t2=﹣3,
综上所述:存在M1(0,2),M2(﹣3,2),M3(2,﹣3),M4(5,﹣18),使得以点A、M、N为顶点的三角形与△ABC相似.
【解析】(1)①先求的直线y= ![]() x+2与x轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x﹣1),然后将点C的坐标代入即可求得a的值;(2)设点P、Q的横坐标为m,分别求得点P、Q的纵坐标,从而可得到线段PQ=
x+2与x轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x﹣1),然后将点C的坐标代入即可求得a的值;(2)设点P、Q的横坐标为m,分别求得点P、Q的纵坐标,从而可得到线段PQ= ![]() m2﹣2m,然后利用三角形的面积公式可求得S△PAC=
m2﹣2m,然后利用三角形的面积公式可求得S△PAC= ![]() ×PQ×4,然后利用配方法可求得△PAC的面积的最大值以及此时m的值,从而可求得点P的坐标;(3)首先可证明△ABC∽△ACO∽△CBO,然后分以下几种情况分类讨论即可:①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;②根据抛物线的对称性,当M(﹣3,2)时,△MAN∽△ABC; ④当点M在第四象限时,解题时,需要注意相似三角形的对应关系.
×PQ×4,然后利用配方法可求得△PAC的面积的最大值以及此时m的值,从而可求得点P的坐标;(3)首先可证明△ABC∽△ACO∽△CBO,然后分以下几种情况分类讨论即可:①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;②根据抛物线的对称性,当M(﹣3,2)时,△MAN∽△ABC; ④当点M在第四象限时,解题时,需要注意相似三角形的对应关系.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小),还要掌握二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国最大的水果公司“佳沃鑫荣懋”旗下子公司“欢乐果园”购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为P=
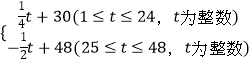 ,且其日销售量y(kg)与时间t(天)的关系如表:
,且其日销售量y(kg)与时间t(天)的关系如表: 时间t(天)
1
3
6
10
20
40
…
日销售量y(kg)
118
114
108
100
80
40
…
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,子公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;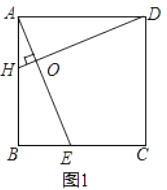
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;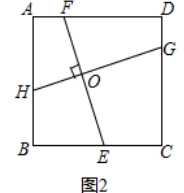
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.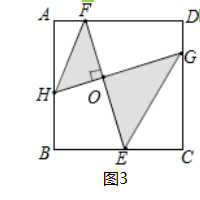
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌
国内品牌
进价(万元/部)
0.44
0.2
售价(万元/部)
0.5
0.25
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.

(1)如图1,当点E、F在线段AD上时,求证:∠DAG=∠DCG;
(2)如图1,猜想AG与BE的位置关系,并加以证明;
(3)如图2,在(2)条件下,连接HO,试说明HO平分∠BHG.
-
科目: 来源: 题型:
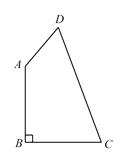
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800
1600
B地区
1600
1200
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
相关试题

