【题目】如图所示是10×8的网格,网格中每个小正方形的边长均为1,A、B两点在小正方形的顶点上,使以A、B、C为顶点的三角形分别满足以下要求: 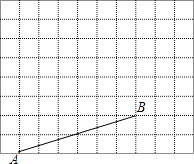
(1)请在图中取一点C(点C必须在小正方形的顶点上),使△ABC为钝角等腰三角形;
(2)通过计算,直接写出△ABC的周长.
参考答案:
【答案】
(1)解:如图所示,△ABC为所求的三角形;
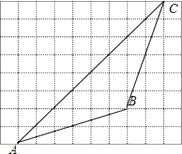
(2)解:由题意得:AB=BC= ![]() =2
=2 ![]() ,
,
AC= ![]() =8
=8 ![]() ,
,
则△ABC周长为4 ![]() +8
+8 ![]()
【解析】(1)如图所示,使AB=BC,连接AC,得到三角形ABC;(2)在网格中,利用勾股定理分别求出AB,BC以及AC的长,即可确定出三角形ABC周长.
【考点精析】根据题目的已知条件,利用等腰三角形的判定和勾股定理的概念的相关知识可以得到问题的答案,需要掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“一个三角形不可能有两个直角”时,第一步应假设:_______________________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF.求证:BD平分∠EBC.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F是四边形ABCD的对角线BD上的两点,BF=DE,AE=CF,∠1=∠2.
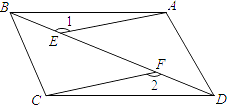
(1)求证:△ABE≌△CDF;
(2)四边形ABCD是平行四边形吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).(供选用的数据:
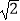 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)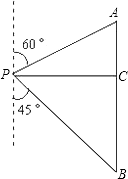
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察、思考、解答: (
 ﹣1)2=(
﹣1)2=(  )2﹣2×1×
)2﹣2×1×  +12=2﹣2
+12=2﹣2  +1=3﹣2
+1=3﹣2 
反之3﹣2 =2﹣2
=2﹣2  +1=(
+1=(  ﹣1)2
﹣1)2
∴3﹣2 =(
=(  ﹣1)2
﹣1)2
∴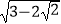 =
=  ﹣1
﹣1
(1)仿上例,化简: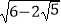 ;
;
(2)若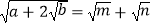 ,则m、n与a、b的关系是什么?并说明理由;
,则m、n与a、b的关系是什么?并说明理由;
(3)已知x=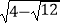 ,求(
,求( 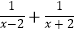 )
) 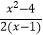 的值(结果保留根号)
的值(结果保留根号)
相关试题

