【题目】阅读理解并在括号内填注理由:
如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
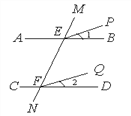
证明:∵AB∥CD,
∴∠MEB=∠MFD(_____________)
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥____.(_______________)
参考答案:
【答案】 两直线平行,同位角相等 MFQ FQ 同位角相等地,两直线平行
【解析】试题分析:由AB与CD平行,利用两直线平行同位角相等得到一对角相等,再由已知角相等,利用等式的性质得到一对同位角相等,可得出EP与FQ平行.
试题解析:证明:∵AB∥CD,
∴∠MEB=∠MFD(两直线平行同位角相等),
又∵∠1=∠2(已知),
∴∠MEB∠1=∠MFD∠2,
即∠MEP=∠MFQ,
∴EP∥FQ(同位角相等两直线平行).
故答案为:两直线平行同位角相等;已知;MFQ;FQ;同位角相等两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一张比例尺是1:50000的地图上,一个多边形区域的面积是320cm2,则该区域的实际面积用科学记数法表示是( )
A.1.6×103m2B.1.6×105 m2C.8×107m2D.8×109m2
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一元二次方程(x﹣2)2﹣x=7x+6化为一般形式是_____,二次项系数是_____,一次项是_____,常数项是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,(10分)AB∥DE,试问∠B、∠E、∠BCE有什么关系.

解:∠B+∠E=∠BCE
过点C作CF∥AB,
则
 ____( )
____( )又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是
A.两个矩形相似B.两个菱形相似
C.两个直角三角形相似D.两个等边三角形相似
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个角的余角比这个角大30°,则这个角的补角是( )
A. 30°B. 150°C. 60°D. 155°
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市120000名初中学生的视力情况,某校数学兴趣小组,并进行整理分析.
(1)小明在眼镜店调查了1000名初中学生的视力,小刚在邻居中调查了20名初中学生的视力,他们的抽样是否合理?并说明理由.
(2)该校数学兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.
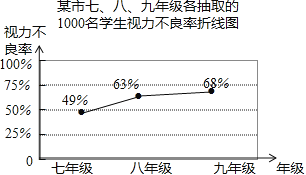
请你根据抽样调查的结果,估计该市120000名初中学生视力不良的人数是多少?
相关试题

