【题目】已知:如图,一次函数y=-2x与二次函数y=ax2+2ax+c的图像交于A、B两点(点A在点B的右侧),与其对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D,点C与点D关于 x轴对称,且△ACD的面积等于2.
① 求二次函数的解析式;
② 在该二次函数图像的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.

参考答案:
【答案】(1)C点的坐标为(-1,2);
(2)①y=2x2+4x; ②点P的坐标为(-1, 10),(-1, ![]() )
)
【解析】(1)由抛物线的对称轴方程可知x=-1,将x=-1代入y=-2x得:y=2,从而可知点C的坐标为(-1,2);
(2)①根据关于x轴对称的坐标特点可知D(-1,-2),从而得到CD=4,然后三角形的面积公式可求得CD边上的高,故此可知得到点A的坐标为(0,0),设抛物线的解析式y=a(x+1)2-2过点A,即可得:a=2,从而得出抛物线的解析式;②利用两个三角形相似求出P点的坐标.
解:(1)∵y=ax2+2ax+c=a(x+1)2+c-a,∴它的对称轴为x=-1.
又∵一次函数y=-2x与对称轴交于点C,∴y=2.
∴C点的坐标为(-1,2).
(2)①∵点C与点D 关于x轴对称,∴点D的坐标为(-1,-2).
∴CD=4,∵△ACD的面积等于2.
∴点A到CD的距离为1,C点与原点重合,点A的坐标为(0,0)
设二次函数为y=a(x+1)2-2过点A,则a=2,
∴y=2x2+4x.
②交点B的坐标为(-3,6).
当△PBD∽△CAD,点P的坐标为(-1, 10),
当△PBD∽△ACD,点P的坐标为(-1,![]() ),
),
∴点P的坐标为(-1, 10),(-1,![]() ).
).
“点睛”本题主要考查的是一次函数、二次函数的综合应用,解答本题主要应用了二次函数的图象的性质、关于x轴对称点的坐标特点、利用相似三角形的性质求出点P的坐标是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3am﹣1bc2和﹣2a3bn﹣2c2是同类项,则m+n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若单项式2xmy3与单项式-3x2yn是同类项,则m-n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(如图(1),在矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F.
(1)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(2)若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;
(3)当射线AF交线段CD于点G时,请直接写出CG的最大值 .


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,E为AC上一点,∠ABE=∠AEB,∠CDE=∠CED. 求证:BE⊥DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额-成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?

-
科目: 来源: 题型:
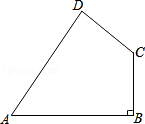
查看答案和解析>>【题目】如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
相关试题

