【题目】如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)△BDE可由△ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法).
参考答案:
【答案】
(1)证明:在Rt△ABC中,
∵∠ABC=90°,
∴∠ABE+∠DBE=90°,
∵BE⊥AC,
∴∠ABE+∠A=90°,
∴∠A=∠DBE,
∵DE是BD的垂线,
∴∠D=90°,
在△ABC和△BDE中,
∵ 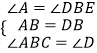 ,
,
∴△ABC≌△BDE(ASA)
(2)解:如图①,点O就是所求的旋转中心.

作法二:如图②,点O就是所求的旋转中心.

【解析】(1)要证△ABC≌△BDE,由已知可知有一组直角相等和一组对应边相等,还需证明一组对应角相等。根据同角的余角相等,即可得证。
(2)方法一、作AB、BD的垂直平分线,两垂直平分线的交点就是旋转中心;方法二、以AB、BD为邻边作正方形,正方形对角线的交点就是所求作的旋转中心。
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于每个非零自然数n,抛物线y=x2﹣
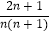 x+
x+  与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2017B2017的值是 .
与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2017B2017的值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
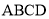 的对角线
的对角线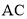 ,
,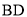 相交于点
相交于点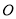 ,
,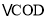 关于
关于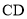 的对称图形为
的对称图形为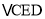 .
. (1)求证:四边形
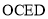 是菱形;
是菱形;(2)连接
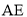 ,交
,交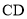 于点
于点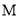 ,连接
,连接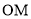 ,取
,取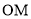 的中点
的中点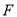 ,连接
,连接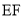 .
.①根据题意补全图形;
②若
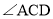 =
=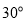 ,请用等式表示线段
,请用等式表示线段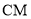 、
、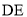 、
、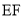 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.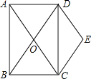
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民低碳生活绿色出行,市政府计划改造如图所示的人行天桥:天桥的高是10米,原坡面倾斜角∠CAB=45°.
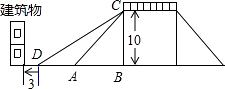
(1)若新坡面倾斜角∠CDB=28°,则新坡面的长CD长是多少?(精确到0.1米)
(2)若新坡角顶点D前留3米的人行道,要使离原坡角顶点A处10米的建筑物不拆除,新坡面的倾斜角∠CDB度数的最小值是多少?(精确到1°) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
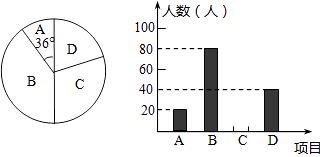
(1)这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
相关试题

