【题目】如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1 , 点P的对应点为P1(a+6,b﹣2 ).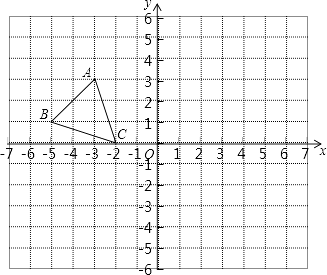
(1)直接写出点A1 , B1 , C1的坐标.
(2)在图中画出△A1B1C1 .
(3)连接A A1 , 求△AOA1的面积.
参考答案:
【答案】
(1)解:∵点P(a,b)的对应点为P1(a+6,b﹣2),
∴平移规律为向右6个单位,向下2个单位,
∴A(﹣3,3),B(﹣5,1),C(﹣2,0)的对应点的坐标为A1(3,1),B1(1,﹣1),C1(4,﹣2);
(2)解:△A1B1C1如图所示;
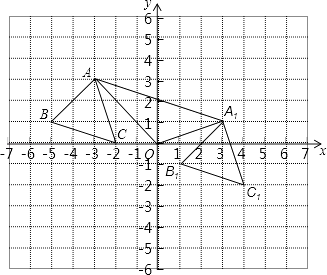
(3)解:△AOA1的面积=6×3﹣ ![]() ×3×3﹣
×3×3﹣ ![]() ×3×1﹣
×3×1﹣ ![]() ×6×2,
×6×2,
=18﹣ ![]() ﹣
﹣ ![]() ﹣6,
﹣6,
=18﹣12,
=6.
【解析】(1)根据点P、P1的坐标确定出平移规律,再求出点A1,B1,C1的坐标即可;
(2)根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;
(3)利用△AOA1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
A.
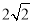 B.
B.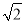 C.
C.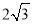 D.
D.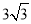
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“任何一个角的补角都不小于这个角”是 命题(填“真”或“假”);若是假命题,举个反例:______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是
A.2013年昆明市九年级学生是总体 B.每一名九年级学生是个体
C.1000名九年级学生是总体的一个样本 D.样本容量是1000
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.
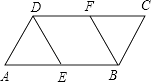
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
2013年,北京发布《2013年至2017年清洁空气行动计划》,北京的空气污染治理目标是力争到2017年全市PM2.5年均浓度比2012年下降25%以上,控制在60微克/立方米左右.
根据某空气监测单位发布数据,2013年北京PM2.5年均浓度89.5微克/立方米,清洁空气问题引起了所有人的高度关注.2014年北京PM2.5年均浓度85.9微克/立方米,比2013年下降3.6微克/立方米.2015年北京PM2.5年均浓度80.6微克/立方米,比上一年又下降了5.3微克/立方米,治理成效比较明显. 2016年北京PM2.5年均浓度73微克/立方米,下降更加明显.
去年11月,北京市通过的《北京市“十三五”时期环境保护和生态环境建设规划》确定的生态环保目标为:2020年,北京市PM2.5年均浓度比2015年下降30%,全市空气质量优良天数比例超过56%.
根据以上材料解答下列问题: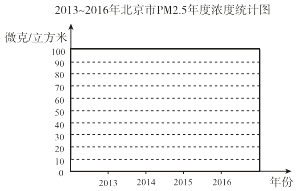
(1)在折线图中表示2013﹣2016年北京市PM2.5年度浓度变化情况,并在图中标明相应数据;
(2)根据绘制的折线图中提供的信息,预估2017年北京市PM2.5年均浓度为 , 你的预估理由是 .
(3)根据《北京市“十三五”时期环境保护和生态环境建设规划》,估计2020年北京市PM2.5年度浓度降至微克/每立方米.(结果保留整数) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,DE∥CA,∠1=∠2,∠3=∠4,∠BAC=84°.求∠EDA的度数.
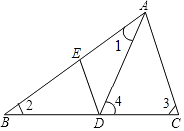
相关试题

