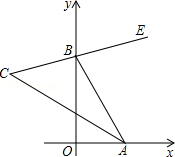
【题目】已知,如图,∠XOY=90°,点A、B分别在射线OX、OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
参考答案:
【答案】∠ACB的大小不发生变化,且始终保持45°.
【解析】
试题分析:根据角平分线的定义、三角形的内角和、外角性质求解.
解:∠C的大小保持不变.理由:
∵∠ABY=90°+∠OAB,AC平分∠OAB,BE平分∠ABY,
∴∠ABE=![]() ∠ABY=
∠ABY=![]() (90°+∠OAB)=45°+
(90°+∠OAB)=45°+![]() ∠OAB,
∠OAB,
即∠ABE=45°+∠CAB,
又∵∠ABE=∠C+∠CAB,
∴∠C=45°,
故∠ACB的大小不发生变化,且始终保持45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b满足|a+3b+1|+(2a﹣4)2=0,则(ab3)2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中假命题是( )
A. 正六边形的外角和等于360°
B. 位似图形必定相似
C. 对角线相等的四边形是矩形
D. 两组对角相等的四边形是平行四边形
-
科目: 来源: 题型:
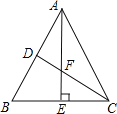
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=x2﹣2x+m的图象与x轴有两个交点,则m的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)
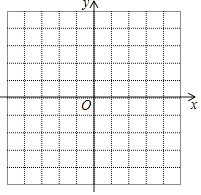
(1)描出A、B、C、D、四点的位置,并顺次连接ABCD,
(2)四边形ABCD的面积是 .
(3)把四边形ABCD向左平移5个单位,再向下平移2个单位得到四边形A'B'C'D',写出点A'、B'、C'、D'的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】近日,记者从潍坊市统计局获悉,2016年第一季度潍坊全市实现生产总值1256.77亿元,将1256.77亿用科学记数法可表示为(精确到百亿位)( )
A.1.2×1011
B.1.3×1011
C.1.26×1011
D.0.13×1012
相关试题

