【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发沿AD向点D匀速运动,速度是1cm/s,过点P作PE∥AC交DC于点E,同时,点Q从点C出发沿CB方向,在射线CB上匀速运动,速度是2cm/s,连接PQ、QE,PQ与AC交与点F,设运动时间为t(s)(0<t<8).
(1)当t为何值时,四边形PFCE是平行四边形;
(2)设△PQE的面积为s(cm2),求s与t之间的函数关系式;
(3)是否存在某一时刻t,使得△PQE的面积为矩形ABCD面积的![]() ;
;
(4)是否存在某一时刻t,使得点E在线段PQ的垂直平分线上.

参考答案:
【答案】(1)![]() (2)s=﹣
(2)s=﹣![]() t2+9t(3)2或6(4)
t2+9t(3)2或6(4)![]()
【解析】
试题分析:(1)四边形PFCE是平行四边形则PD=CQ,据此即可得到关于t的方程,即可求解;
(2)用t表示出PD、EC、DE、CQ的长,则四边形DPQC、△PDE以及△QCE的面积可用t表示,则进一步表示出△PQE的面积,从而得到函数解析式;
(3)根据△PQE的面积为矩形ABCD面积的![]() 即可列方程求解;
即可列方程求解;
(4)点E在线段PQ的垂直平分线上,则PE=QE,然后根据勾股定理表示出PE2和QE2,即可列方程求得t的值.
试题解析:(1)PD=8﹣t,CQ=2t,
根据题意得:8﹣t=2t,
解得:t=![]() ;
;
(2)![]() =
=![]() (PD+CQ)·CD=
(PD+CQ)·CD=![]() ×6(8﹣t+2t)=3(8+t)=3t+24,
×6(8﹣t+2t)=3(8+t)=3t+24,
∵PE∥AC,
∴![]() ,
,
∴![]() ,
,
则DE=﹣![]() t+6,
t+6,
则EC=6﹣(﹣![]() t+6)=
t+6)=![]() t,
t,
则![]() =
=![]() PD·DE=
PD·DE=![]() (8﹣t)·(﹣
(8﹣t)·(﹣![]() t+6),
t+6),
![]() =
=![]() CQ·EC=
CQ·EC=![]() ×2t·
×2t·![]() t=
t=![]() t2,
t2,
则s=3t+24﹣![]() (8﹣t)·(﹣
(8﹣t)·(﹣![]() t+6)﹣
t+6)﹣![]() t2,
t2,
即s=﹣![]() t2+9t;
t2+9t;
(3)![]() =6×8=48,
=6×8=48,
根据由题意得:﹣![]() t2+9t=
t2+9t=![]() ×48,
×48,
解得:t=2或6;
(4)在直角△PDE中,PE2=(8﹣t)2+(﹣![]() t+6)2,
t+6)2,
在直角△COQ中,QE2=(2t)2+(![]() t)2,
t)2,
当点E在线段PQ的垂直平分线上时,PE2=QE2,
则(8﹣t)2+(﹣![]() t+6)2=(2t)2+(
t+6)2=(2t)2+(![]() t)2,
t)2,
解得:t=![]() 或
或![]() (舍去).
(舍去).
则t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(x+1)(x﹣4)+3x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)。
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
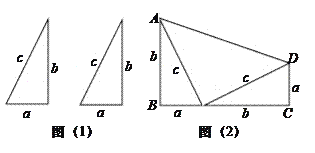
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛,对这两名运动员进行了10次测试,经过数据分析,甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024(s2),乙的方差为0.008(s2),则这10次测试成绩比较稳定的是 运动员.(填“甲”或“乙”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年上半年,天津市生产总值8500.91亿元,按可比价格计算,同步增长9.2%,将“8500.91”用科学记数法可表示为( )
A.8.50091×103
B.8.50091×1011
C.8.50091×105
D.8.50091×1013 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)( ﹣
﹣  +
+ 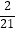 )×(﹣63);
)×(﹣63);
(2)(﹣2)2﹣5×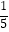 +|﹣2|
+|﹣2|
(3) +
+ 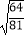 ﹣|﹣2|
﹣|﹣2|
(4)﹣14﹣ ×[3﹣(﹣3)2]
×[3﹣(﹣3)2]
(5)﹣22+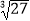 ﹣6÷(﹣2)×
﹣6÷(﹣2)× 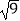 .
. -
科目: 来源: 题型:
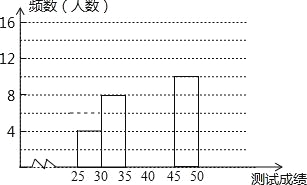
查看答案和解析>>【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别
成绩x分
频数(人数)
第1组
25≤x<30
4
第2组
30≤x<35
8
第3组
35≤x<40
16
第4组
40≤x<45
a
第5组
45≤x<50
10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
相关试题

