Question

【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．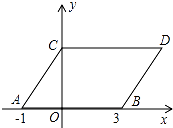

（1）求点C，D的坐标；
（2）若在y轴上存在点 M，连接MA，MB，使S△MAB=S平行四边形ABDC ， 求出点M的坐标．
（3）若点P在直线BD上运动，连接PC，PO．
①若P在线段BD之间时（不与B，D重合），求S△CDP+S△BOP的取值范围；
②若P在直线BD上运动，请直接写出∠CPO、∠DCP、∠BOP的数量关系．

Answer 1

【答案】
（1）解：由平移可知：C（0，2），D（4，2）
（2）解：∵AB=4，CO=2，

∴S平行四边形ABOC=ABCO=4×2=8，

设M坐标为（0，m），

∴ ×4×|m|=8，解得m=±4

∴M点的坐标为（0，4）或（0，﹣4）

（3）解：①S梯形OCDB= ×（3+4）×2=7，

当点P运动到点B时，S△BOC最小，S△BOC的最小值= ×3×2=3，S△CDP+S△BOP＜4，

当点P运动到点D时，S△BOC最大，S△BOC的最大值= ×4×2=4，S△CDP+S△BOP＞3，

所以3＜S△CDP+S△BOP＜4；

②当点P在BD上，如图1，作PE∥CD，

∵CD∥AB，

∴CD∥PE∥AB，

∴∠DCP=∠EPC，∠BOP=∠EPO，

∴∠DCP+∠BOP=∠EPC+∠EPO=∠CPO；

当点P在线段BD的延长线上时，如图2，作PE∥CD，

∵CD∥AB，

∴CD∥PE∥AB，

∴∠DCP=∠EPC，∠BOP=∠EPO，

∴∠EPO﹣∠EPC=∠BOP﹣∠DCP，

∴∠BOP﹣∠DCP=∠CPO；

同理可得当点P在线段DB的延长线上时，∠DCP﹣∠BOP=∠CPO

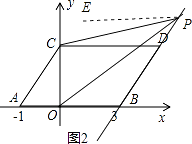
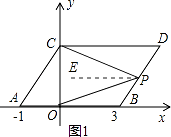
【解析】（1）根据点的平移规律易得点C，D的坐标；（2）先计算出S平行四边形ABOC=8，设M坐标为（0，m），根据三角形面积公式得 ×4×|m|=8，解得m=±4，于是可得M点的坐标为（0，4）或（0，﹣4）；（3）①先计算出S梯形OCDB=7，再讨论：当点P运动到点B时，S△BOC的最小值=3，则可判断S△CDP+S△BOP＜4，当点P运动到点D时，S△BOC的最大值=4，于是可判断S△CDP+S△BOP＞3，所以3＜S△CDP+S△BOP＜4；②分类讨论：当点P在BD上，如图1，作PE∥CD，根据平行线的性质得CD∥PE∥AB，则∠DCP=∠EPC，∠BOP=∠EPO，易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO；当点P在线段BD的延长线上时，如图2，同样有∠DCP=∠EPC，∠BOP=∠EPO，由于∠EPO﹣∠EPC=∠BOP﹣∠DCP，于是∠BOP﹣∠DCP=∠CPO；同理可得当点P在线段DB的延长线上时，∠DCP﹣∠BOP=∠CPO．
【考点精析】关于本题考查的三角形的面积，需要了解三角形的面积=1/2×底×高才能得出正确答案．