【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;

(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
参考答案:
【答案】解:(1)∵90÷30%=300(名),
∴一共调查了300名学生。
(2)艺术的人数:300×20%=60名,其它的人数:300×10%=30名。
补全折线图如下:
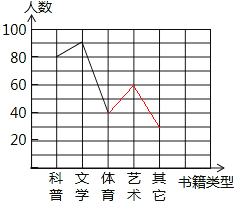
(3)体育部分所对应的圆心角的度数为:![]() ×360°=48°。
×360°=48°。
(4)∵1800×![]() =480(名),
=480(名),
∴1800名学生中估计最喜爱科普类书籍的学生人数为480。
【解析】
试题(1)用文学的人数除以所占的百分比计算即可得解。
(2)根据所占的百分比求出艺术和其它的人数,然后补全折线图即可。
(3)用体育所占的百分比乘以360°,计算即可得解。
(4)用总人数乘以科普所占的百分比,计算即可得解。
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出一组式子:32+42=52,82+62=102,152+82=172,242+102=262……
(1)你能发现上式中的规律吗?
(2)请你接着写出第五个式子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个四边形的边角料,东东通过测量,获得了如下数据:AB=3cm,BC=12cm,CD=13cm,AD=4cm,东东由此认为这个四边形中∠A恰好是直角,你认为东东的判断正确吗?如果你认为他正确,请说明其中的理由;如果你认为他不正确,那你认为需要什么条件,才可以判断∠A是直角?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
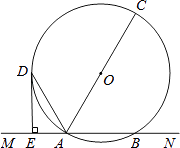
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+2x+c经过点A(0,3)、B(﹣1,0),请解答下列问题:
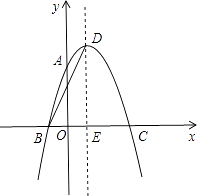
(1)求抛物线的解析式;
(2)抛物线的顶点为D,与x轴的另一交点为C,对称轴交x轴于点E,连接BD,求cos∠DBE;
(3)在直线BD上是否存在点F,使由B、C、F三点构成的三角形与△BDE相似?若存在,求出点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接四边形各边中点,所得的图形是__________。顺次连接对角线______________的四边形的各边中点所得的图形是矩形。顺次连接对角线_________的四边形的各边中点所得的四边形是菱形。顺次连接对角线_________的四边形的各边中点所得的四边形是正方形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

相关试题

