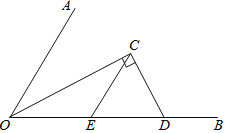
【题目】如图,![]() ,OC平分
,OC平分![]() ,C为角平分线上一点,过点C作
,C为角平分线上一点,过点C作![]() ,垂足为C,交OB于点D,
,垂足为C,交OB于点D,![]() 交OB于点E.
交OB于点E.
![]() 判断
判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 若
若![]() ,求CD的长.
,求CD的长.
参考答案:
【答案】(1)等边三角形(2)![]()
【解析】
(1)△CED为等边三角形,理由如下:由OC为角平分线及∠AOB度数求出∠AOC与∠COE度数,再由CE与OA平行,得到一对内错角相等,再由CD与OC垂直,求出∠ECD度数,利用三个内角相等的三角形为等边三角形即可得证;
(2)由△CED为等边三角形,得到三边相等,利用等角对等边得到OE=CE,进而得到OE=CE=DE,设CD=x,利用30度角所对的直角边等于斜边的一半得到OD=2x,再由OC的长,利用勾股定理列出方程,求出方程的解得到x的值,即可确定出CD的长.
![]() 是等边三角形,理由如下:
是等边三角形,理由如下:
![]() 平分
平分![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形;
是等边三角形;
![]() 是等边三角形,
是等边三角形,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,根据勾股定理得:
中,根据勾股定理得:![]() ,
,
解得:![]() ,
,
则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份
4月
5月
6月
用水量
15
17
21
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
 有两个正整数根
有两个正整数根 是正整数
是正整数 的三边a、b、c满足
的三边a、b、c满足 ,
, ,
, .
.求:
 的值;
的值; 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球.两次都摸到红球的概率是( )
A.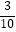
B.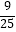
C.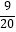
D.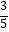
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
,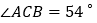 ,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,求
,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,求 、
、 和
和 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上A点表示数
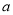 ,B点表示数
,B点表示数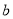 ,且
,且 、
、 满足
满足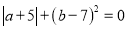 ,
, 
(1)点A表示的数为_______;点B表示的数为__________;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=3BC,则C点表示的数__________;
(3)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请分别表示出甲、乙两小球到原点的距离(用含t的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是以原点为圆心,
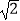 为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )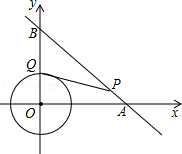
A.3
B.4
C.6﹣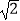
D.3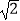 ﹣1
﹣1
相关试题

