【题目】如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DECD,正确的有( ) 
A.2个
B.3个
C.4个
D.5个
参考答案:
【答案】C
【解析】解:连接OE,如图所示:
∵AD与圆O相切,DC与圆O相切,BC与圆O相切,
∴∠DAO=∠DEO=∠OBC=90°,
∴DA=DE,CE=CB,AD∥BC,
∴CD=DE+EC=AD+BC,选项②正确;
在Rt△ADO和Rt△EDO中, ![]() ,
,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,即∠DOC=90°,选项①正确;
∴∠DOC=∠DEO=90°,又∠EDO=∠ODC,
∴△EDO∽△ODC,
∴ ![]() =
= ![]() ,即OD2=DCDE,选项⑤正确;
,即OD2=DCDE,选项⑤正确;
∵∠AOD+∠COB=∠AOD+∠ADO=90°,
∠A=∠B=90°,
∴△AOD∽△BOC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,选项③正确;
,选项③正确;
同理△ODE∽△OEC,
∴ ![]() ,选项④错误;
,选项④错误;
故选C.

连接OE,由AD,DC,BC都为圆的切线,根据切线的性质得到三个角为直角,且利用切线长定理得到DE=DA,CE=CB,由CD=DE+EC,等量代换可得出CD=AD+BC,选项②正确;由AD=ED,OD为公共边,利用HL可得出直角三角形ADO与直角三角形EDO全等,可得出∠AOD=∠EOD,同理得到∠EOC=∠BOC,而这四个角之和为平角,可得出∠DOC为直角,选项①正确;由∠DOC与∠DEO都为直角,再由一对公共角相等,利用两对对应角相等的两三角形相似,可得出三角形DEO与三角形DOC相似,由相似得比例可得出OD2=DECD,选项⑤正确;由△AOD∽△BOC,可得 ![]() =
= ![]() =
= ![]() =
= ![]() ,选项③正确;由△ODE∽△OEC,可得
,选项③正确;由△ODE∽△OEC,可得 ![]() ,选项④错误.
,选项④错误.
-
科目: 来源: 题型:
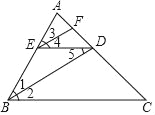
查看答案和解析>>【题目】如图,BD是∠ABC的平分线,ED∥BC,∠4=∠5,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2( )
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥ ( )
∴∠3=∠1( )
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
-
科目: 来源: 题型:
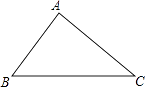
查看答案和解析>>【题目】如图,在△ABC中,BC=10,∠B=60°,∠C=45°,则点A到BC的距离是( )
A.10﹣5
B.5+5
C.15﹣5
D.15﹣10
-
科目: 来源: 题型:
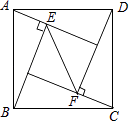
查看答案和解析>>【题目】如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
A.7
B.8
C.7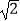
D.7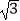
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,AB=5, AE平分∠DAB交BC所在直线于点E,CE=2,则AD=_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=50° ,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)若AB=4,求
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AB C中,AB=AC,BD和CD分别是∠ABC和∠ACB的平分线,EF过D点,且EF∥BC,图中等腰三角形共有( )

A. 2个 B. 3个 C. 4个 D. 5个
相关试题

