【题目】在△ABC中,AB=AC,∠BAC=50° ,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)若AB=4,求![]() 的值.
的值.

参考答案:
【答案】(1)20°;(2)32.
【解析】
(1)根据等腰直角三角形的旋转得出∠ABE=∠AEB,求出∠BAE,根据三角形内角和定理求出即可;
(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(3)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2,即可得出答案.
(1)∵AB=AC,AC=AE.
∴AB=AE,
∴∠AEB=∠ABE.
∵∠BAC=50°,∠CAE=90°,
∴∠BAE=50°+90°=140°.
∴∠AEB=![]() .
.
(2)∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
∴△ABF≌△ACF.
∴∠ABF=∠ACF.
∵∠AEB=∠ABE,
∴∠AEB=∠ACF.
(3)∵∠AEB=∠ACF ,∠AGE=∠CGF,
∴∠CFE=∠CAE=90°.
∴![]() .
.
∵CF=BF,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
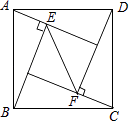
A.7
B.8
C.7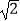
D.7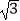
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DECD,正确的有( )

A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,AB=5, AE平分∠DAB交BC所在直线于点E,CE=2,则AD=_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AB C中,AB=AC,BD和CD分别是∠ABC和∠ACB的平分线,EF过D点,且EF∥BC,图中等腰三角形共有( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明爸爸装修要粉刷断居室的墙面,在家装商场选购某品牌的乳胶漆:
规格(升/桶)
价格(元/桶)
大桶装
18
225
小桶装
5
90
小明爸估算家里的粉刷面积,若买“大桶装”,则需若干桶但还差2升;若买“小桶装”,则需多买11桶但会剩余1升,
(1)小明爸预计墙面的粉刷需要乳胶漆多少升?
(2)喜迎新年,商场进行促销:满1000减120元现金,并且该品牌商家对“小桶装”乳胶漆有“买4送1“的促销活动,小明爸打算购买“小桶装”,比促销前节省多少钱?
(3)在(2)的条件下,商家在这次乳胶漆的销售买卖中,仍可盈利25%,则小桶装乳胶漆每桶的成本是多少元?
相关试题

