【题目】如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为 ![]() ,且点P在图中阴影部分(包括边界)运动.若
,且点P在图中阴影部分(包括边界)运动.若 ![]() ,其中x,y∈R,则4x﹣y的最大值为( )
,其中x,y∈R,则4x﹣y的最大值为( ) 
A.![]()
B.![]()
C.2
D.![]()
参考答案:
【答案】B
【解析】解:以A为坐标原点,AB为x轴,AD为y轴建立平面直角坐标系,则 A(0,0),D(0,1),C(1,1),B(2,0),
直线BD的方程为x+2y﹣2=0,C到BD的距离d= ![]()
∴圆弧以点C为圆心的圆方程为(x﹣1)2+(y﹣1)2= ![]() ,
,
设P(m,n)则 ![]() =(m,n),
=(m,n),![]() =(0,1),
=(0,1), ![]() =(2,0),
=(2,0), ![]() =(﹣1,1)
=(﹣1,1)
若 ![]() ,
,
∴(m,n)=(2x﹣y,y)
∴m=2x﹣y,n=y
∵P在圆内或圆上
∴(2x﹣y﹣1)2+(y﹣1)2≤ ![]() ,
,
设4x﹣y=t,则y=4x﹣t,代入上式整理得80x2﹣(48t+32)x+8t2+7≤0,
设f(x)=80x2﹣(48t+32)x+8t2+7≤0,x∈[ ![]() ,
, ![]() ],
],
则  ,
,
解得2≤t≤3+ ![]() ,
,
故4x﹣y的最大值为3+ ![]() ,
,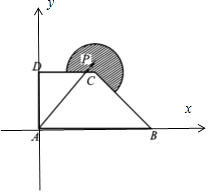
故选:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】
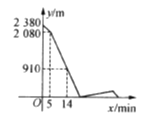
 两地之间的路程为2 380 m,甲、乙两人分别从
两地之间的路程为2 380 m,甲、乙两人分别从 两地出发,相向而行.已知甲先出发5 min后,乙才出发,他们两人在
两地出发,相向而行.已知甲先出发5 min后,乙才出发,他们两人在 之间的
之间的 地相遇,相遇后,甲立即返回
地相遇,相遇后,甲立即返回 地,乙继续向
地,乙继续向 地前行.甲到达
地前行.甲到达 地时停止行走,乙到达
地时停止行走,乙到达 地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程
地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程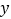 (m)与甲出发的时间
(m)与甲出发的时间 (min)之间的关系如图所示,则乙到达
(min)之间的关系如图所示,则乙到达 地时,甲与
地时,甲与 地相距的路程是
地相距的路程是________m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2cos(ωx﹣φ)(ω>0,φ∈[0,π]的部分图象如图所示,若A(
 ,
,  ),B(
),B(  ,
,  ),则函数f(x)的单调增区间为( )
),则函数f(x)的单调增区间为( ) 
A.[﹣ +2kπ,
+2kπ,  +2kπ](k∈Z)
+2kπ](k∈Z)
B.[ +2kπ,
+2kπ,  +2kπ](k∈Z)
+2kπ](k∈Z)
C.[﹣ +kπ,
+kπ,  +kπ](k∈Z)
+kπ](k∈Z)
D.[ +kπ,
+kπ,  +kπ](k∈Z)
+kπ](k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥P﹣ABC的三条侧棱两两垂直,且PA=PB=PC=1,则其外接球上的点到平面ABC的距离的最大值为( )
A.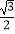
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,关于x的不等式f2(x)+af(x)>0只有两个整数解,则实数a的取值范围为 .
,关于x的不等式f2(x)+af(x)>0只有两个整数解,则实数a的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足
 .
.
(1)求△ABC的面积;
(2)若tanB=2,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图3所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.

(1)求当天的利润y(单位:元)关于当天需求量n(单位:个,n∈N)的函数解析式;
(2)求当天的利润不低于750元的概率.
相关试题

