【题目】如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE. 
(1)求证:DE是⊙O的切线.
(2)填空: ①当∠CAB=时,四边形AOED是平行四边形;
②连接OD,在①的条件下探索四边形OBED的形状为 .
参考答案:
【答案】
(1)解:连接OD,
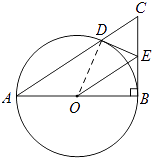
∵E是BC的中点,
O是AB的中点,
∴OE是△ABC的中位线,
∴OE∥AC,
∠BOE=∠BAC,
∠DOE=∠ADO,
∵OD=OA,
∴∠BAC=∠ADO,
∴∠BOE=∠DOE,
在△DOE与△BOE中,
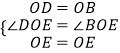 ,
,
∴△DOE≌△BOE,
∴∠OBE=∠ODE=90°,
∴DE是⊙O的切线
(2)45°;正方形
【解析】解:(2)①当∠CAB=45°时, ∴∠ADO=45°,
∴∠AOD=90°,
又∵∠EDO=90°,
∴DE∥AB,
∵OE∥AC,
∴四边形AOED是平行四边形;
②由①可知:∠EDO=∠DOB=∠ABC=90°,
∴四边形OBED是矩形,
∵OD=OB,
∴矩形OBED是正方形.
所以答案是:①45°;②正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3 在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为 .
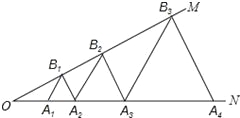
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1 , S2 , 则S2﹣S1= .
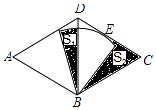
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只跳蚤在一数轴上从原点开始,第1次向右跳1个单位长度,紧接着第2次向左跳2个单位长度,第3次向右跳3个单位长度,第4次向左跳4个单位长度,…,依此规律跳下去,当它跳第100次落下时,所在位置表示的数是( )
A. 50 B. -50 C. 100 D. -100
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-15)÷(-3);
(2)(-12)÷(-
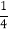 );
);(3)(-0.75)÷0.25;
(4)(-12)÷(-
 )÷(-100).
)÷(-100). -
科目: 来源: 题型:
查看答案和解析>>【题目】决心试一试,请阅读下列材料:计算:

解法一:原式=

=

=

解法二:原式=

=

=

=

解法三:原式的倒数为:

=

=﹣20+3﹣5+12
=﹣10
故原式 =

上述得出的结果不同,肯定有错误的解法,你认为解法 是错误的,在正确的解法中,你认为解法 最简捷.然后请解答下列问题,计算:
 .
. -
科目: 来源: 题型:
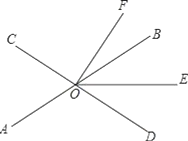
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
相关试题

