【题目】解答
(1)求不等式 ![]() ﹣
﹣ ![]() ≤
≤ ![]() 的非负整数解;
的非负整数解;
(2)若关于x的方程2x﹣3m=2m﹣4x+4的解不小于 ![]() ﹣
﹣ ![]() ,求m的最小值.
,求m的最小值.
参考答案:
【答案】
(1)解:原不等式可化为: ![]() ﹣﹣
﹣﹣ ![]() ≤
≤ ![]() ,
,
去分母,得6(4x﹣10)﹣15(5﹣x)≤10(3﹣2x),
去括号,得24x﹣60﹣75+15x≤30﹣20x,
移项,得24x+15x+20x≤30+60+75,
合并同类项,得59x≤165,
把系数化为1,得x≤ ![]() ,
,
所以原不等式的非负整数解是:0,1,2
(2)解:关于x的方程2x﹣3m=2m﹣4x+4的解为:x= ![]() .
.
根据题意,得 ![]() ≥
≥ ![]() ﹣
﹣ ![]() ,
,
去分母,得4(5m+4)≥21﹣8(1﹣m),
去括号,得20m+16≥21﹣8+8m,
移项,合并同类项得12m≥﹣3,
系数化为1,得m≥﹣ ![]() .
.
所以当m≥﹣ ![]() 时,方程的解不小于
时,方程的解不小于 ![]() ﹣
﹣ ![]() ,
,
所以m的最小值为﹣ ![]()
【解析】(1)首先利用分数的基本性质,将分子、分母上的小数化成整数,然后根据不等式的性质2去掉分母等进行求解不等式,再在解集中求出符合条件的非负整数;(2)首先求解关于x的方程2x﹣3m=2m﹣4x+4,即可求得x的值,根据方程的解的解不小于 ![]() ﹣
﹣ ![]() ,即可得到关于m的不等式,即可求得m的范围,从而求解.
,即可得到关于m的不等式,即可求得m的范围,从而求解.
【考点精析】解答此题的关键在于理解一元一次不等式的整数解的相关知识,掌握大大取较大,小小取较小;小大,大小取中间;大小,小大无处找.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是( )

A.15cm
B.13cm
C.11cm
D.9cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=
 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 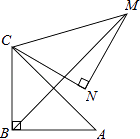
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 有一个角是直角的四边形是矩形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直平分的四边形是正方形
D. 两条对角线相等的菱形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】“夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.
(1)求普通床位和高档床位每月收费各多少元?
(2)根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过实际入住普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)90°﹣17°27′
(2)(﹣1)100×5+(﹣2)4÷4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣2x+3=0的一次项和常数项分别是( )
A.2和3B.﹣2和3C.﹣2x和3D.2x和3
相关试题

