【题目】如图①所示,直线L:y=mx+5m与x轴负半轴,y轴正半轴分别交于A、B两点.
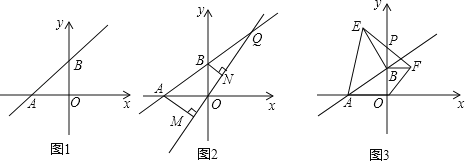
(1)当OA=OB时,求点A坐标及直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=4,求BN的长;
(3)当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图③.
问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值?若是,请求出其值;若不是,说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)是,
;(3)是,![]()
【解析】
(1)由直线L解析式,求出![]() 与
与![]() 的坐标,根据
的坐标,根据![]() ,求出
,求出![]() 的值,即可确定出直线L解析式.
的值,即可确定出直线L解析式.
(2)由![]() ,对顶角相等,且一对直角相等,利用
,对顶角相等,且一对直角相等,利用![]() 得到
得到![]() ,用对应线段相等求长度;
,用对应线段相等求长度;
(3)如图,作![]() 轴于
轴于![]() 点,利用
点,利用![]() 得到
得到![]() ,利用全等三角形对应边相等得到
,利用全等三角形对应边相等得到![]() ,再利用
,再利用![]() 得到
得到![]() ,寻找相等线段,并进行转化,求
,寻找相等线段,并进行转化,求![]() 的长.
的长.
(1)∵直线L:![]() ,
,
∴![]() ,
,
由![]() ,得
,得![]() ,
,
∴直线L的解析式为:![]() ;
;
(2)![]()
∴![]()
又![]()
∴![]()
在△AMO与![]() 中,
中,
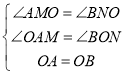 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
答案是:![]()
(3)如图,作![]() 轴于
轴于![]() 点,
点,
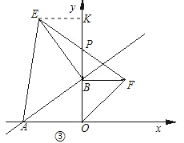
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() °,
°,
∴![]() °,
°,
∵![]() °,
°,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
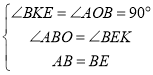 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
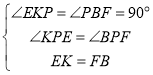 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点A、B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A、B,且a、m满足2a﹣m=d(d为常数).
(1)若一次函数y1=kx+b的图象经过A、B两点.
①当a=1、d=﹣1时,求k的值;
②若y随x的增大而减小,求d的取值范围;
(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;
(3)点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是菱形
是菱形 的对角线
的对角线 、
、 的交点,
的交点, 、
、 分别是
分别是 、
、 的中点.下列结论:①
的中点.下列结论:① ;②四边形
;②四边形 也是菱形;③四边形
也是菱形;③四边形 的面积为
的面积为 ;④
;④ ;⑤
;⑤ 是轴对称图形.其中正确的结论有( )
是轴对称图形.其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①:要设计一幅宽
 ,长
,长 的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为
的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为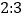 ,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?由横、竖彩条的宽度比为
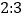 ,可设每个横彩条的宽为
,可设每个横彩条的宽为 ,则每个竖彩条的宽为
,则每个竖彩条的宽为 .为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形
.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形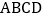 .
.结合以上分析完成填空:
如图②:用含
 的代数式表示:
的代数式表示: ________
________ ;
; ________
________ ;矩形
;矩形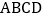 的面积为________
的面积为________ ;列出方程并完成本题解答.
;列出方程并完成本题解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A.
 B. 2
B. 2 -
- C. 2
C. 2 -
- D. 4
D. 4 -
-
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,过对角线
中,过对角线 上一点
上一点 作
作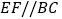 ,
, ,且
,且 ,
, ,则
,则 ( )
( )
A. 3 B. 4 C. 5 D. 6
相关试题

