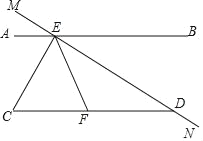
【题目】如图,∠AEM=30°,CE⊥MN,垂足为点E,∠CDN=150°,EC平分∠AEF.
(1)求∠C的度数;
(2)求证:∠FDE=∠FED.
参考答案:
【答案】(1) ∠C=60°;(2)见解析.
【解析】
(1)由垂直可得∠AEC=60°,又由∠CDE和∠CDN互补可得∠CDE=30°,则AB∥CD,根据两直线平行同位角相等则∠C=60°.(2)由角平分线可得∠AEC=∠CEF,再由平角180°,求出∠FED=30°,等量代换得∠FED=∠EDF.
证明:(1)∵CE⊥MN,(已知),
∴∠MEC=90°,( 垂直定义),
∵∠AEM=30°,
∴∠AEC=∠MEC﹣∠AEM=90°﹣30°=60°,
∵∠CDE+∠CDN=180°(平角的定义),
∠CDN=150°,
∴∠CDE=180°﹣∠CDN=180°﹣150°=30°,
∴∠CDE=∠AEM(等量代换),
∴AB∥CD(同位角相等,两直线平行),
∴∠C=∠AEC(两直线平行,内错角相等),
即∠C=60°,
(2)∵EC平分∠AEF.(已知),
∴∠AEC=∠CEF(角平分线的定义),
∠FED=180°﹣∠AEC﹣∠CEF﹣∠AEM=180°﹣60°﹣60°﹣30°=30°,
∴∠FED=∠EDF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在
 的正半轴上,点B的坐标为(3,4)一次函数
的正半轴上,点B的坐标为(3,4)一次函数 的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.
的图象与边OC、AB分别交于点D、E,并且满足OD= BE.点M是线段DE上的一个动点.(1)求b的值;
(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是
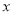 轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
-
科目: 来源: 题型:
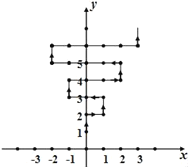
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(0,1),(0,2),(1,2),(1,3),(0,3),(﹣1,3)…,根据这个规律探索可得,第90个点的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承优秀传统文化,我市组织了一次七年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
组别
成绩分组
频数
频率
A
35≤x<38
3
0.03
B
38≤x<41
a
0.12
C
41≤x<44
20
0.20
D
44≤x<47
35
0.35
E
47≤x≤50
30
b
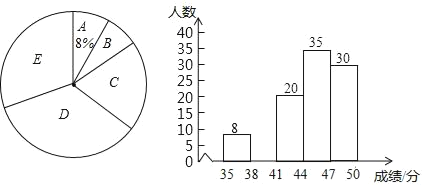
请根据所提供的信息解答下列问题:
(1)频率统计表中a= ,b= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中D组的圆心角是 度;
(4)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?
-
科目: 来源: 题型:
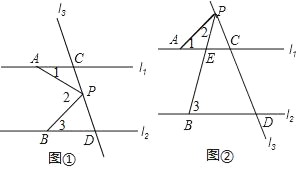
查看答案和解析>>【题目】如图①,已知直线l1、l2,直线l3和直线l1、l2交于点C和D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系 ;
(2)如图②如果l1∥l2,点P在直线l1的上方运动时,试猜想∠1+∠2与∠3之间关系并给予证明;
(3)如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
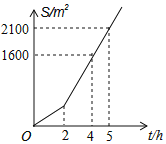
A. 200B. 300C. 400D. 500
相关试题

