【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 上的动点(不与
上的动点(不与![]() 重合).过
重合).过![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .设
.设![]() 的长度为
的长度为![]() ,
,![]() 与
与![]() 的长度和为
的长度和为![]() .则能表示
.则能表示![]() 与
与![]() 之间的函数关系的图象大致是( )
之间的函数关系的图象大致是( )
A.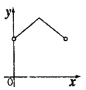 B.
B.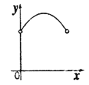 C.
C.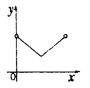 D.
D.
参考答案:
【答案】D
【解析】
根据三角形面积得出S△PAB=![]() PEAB;S△PAB=S△PQB+S△PAQ=
PEAB;S△PAB=S△PQB+S△PAQ=![]() QNPB+
QNPB+![]() PAMQ,进而得出y=
PAMQ,进而得出y=![]() ,即可得出答案.
,即可得出答案.
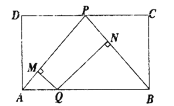
解:连接PQ,作PE⊥AB垂足为E,
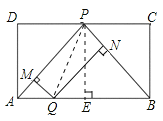
∵过Q作QM⊥PA于M,QN⊥PB于N,
∴S△PAB=![]() PEAB;
PEAB;
S△PAB=S△PQB+S△PAQ=![]() QNPB+
QNPB+![]() PAMQ,
PAMQ,
∵矩形ABCD中,P为CD中点,
∴PA=PB,
∵QM与QN的长度和为y,
∴S△PAB=S△PQB+S△PAQ=![]() QNPB+
QNPB+![]() PAMQ=
PAMQ=![]() PB(QM+QN)=
PB(QM+QN)=![]() PBy,
PBy,
∴S△PAB=![]() PEAB=
PEAB=![]() PBy,
PBy,
∴y=![]() ,
,
∵PE=AD,
∴PE,AB,PB都为定值,
∴y的值为定值,符合要求的图形为D,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
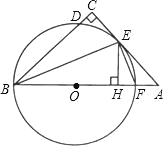
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为4时,m的值是_____.当点B的横坐标为4n(n为正整数)时,m=_____(用含n的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在阳光体育活动时间,小亮、小莹、小芳到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余两人中随机选取一人打第一场,选中小莹的概率是________.
(2)如果确定小亮打第一场,用投掷硬币的方法确定小莹、小芳谁打第一场,并决定小亮做裁判,由小亮抛掷一枚硬币,规定正面朝上小莹胜,反面朝上小芳胜,最终胜两局以上者(包括两局)打第一场.小亮第一次投掷的结果是正面朝上,请用列表或画树状图的方法表示最后两次投掷硬币的所有情况,并求小芳打第一场的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面的两位数18, 27,36, 45,54,63,72,81,99都是9的整数倍,小明发现这些数的个位数字与十位数字的和也都是9的整数倍,例如18的的个位数字8与十位数字1的和是9.于是小明有了这样的结论:个位数字与十位数字的和是9的倍数的两位数一定是9的倍数.小明经过思考后给出了如下的证明:
设十位上的数字为
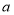 ,个位上的数字为
,个位上的数字为 ,并且
,并且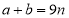 (
(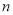 为正整数)
为正整数)那么这个两位数可表示为
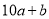
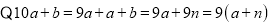
∴这个两位数是9的倍数
小明猜想:个位数字与十位数字与百位数字的和是9的倍数的三位数也一定是9的倍数.小明的这个猜想的结论是否正确?若正确模仿小明的证明思路给出证明,若不正确举出反例.
相关试题

