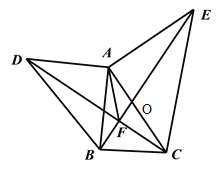
【题目】如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE。连结DC、BE交于F点。

(1)求证:△DAC≌△BAE;
(2)求证:DC⊥BE;
(3)求证:∠DFA=∠EFA.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)由题意可得AD=AB,AC=AE,由∠DAB=∠CAE=90°,可得到∠DAC=∠BAE,从而可证△DAC≌△BAE;
(2)由(1)可得∠ACD=∠AEB,再利用直角三角形的性质及等量代换即可得到结论;
(3)作AM⊥DC于M,AN⊥BE于N,利用全等三角形的面积相等及角平分线的判定即可证得结论.
证明:(1)∵![]()
![]() ,
,
∴![]() ,
,
即![]() ,
,
又∵![]() ,AC=AE,
,AC=AE,
∴△DAC≌△BAE;
(2)∵△DAC≌△BAE,
∴∠ACD=∠AEB,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
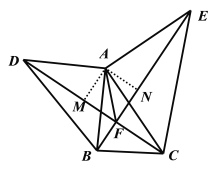
∵![]() ≌
≌![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的平分线,
的平分线,
即![]() .
.
故答案为:(1)证明见解析;(2)证明见解析;(3)证明见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.
 (保留作图痕迹,不要求写作法和证明);
(保留作图痕迹,不要求写作法和证明);(2)在(1)条件下,连结BD,当BC=3cm,AB=5cm时,求△BCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,点
中,点 在
在 边所在直线上(与点
边所在直线上(与点 ,
, 不重合),点
不重合),点 在
在 边所在直线上,且
边所在直线上,且 ,
, 交
交 边于点
边于点 .
.
(1)如图1,若
 是等边三角形,点
是等边三角形,点 在
在 边上,过点
边上,过点 作
作 于
于 ,试说明:
,试说明: .
.某同学发现可以由以下两种思路解决此问题:
思路一:过点
 作
作 ,交
,交 于点
于点 ,如图1
,如图1因为
 是等边三角形,得
是等边三角形,得 是等边三角形
是等边三角形又由
 ,得
,得

再说明


得出
 .
.从而得到结论.
思路二:过点
 作
作 ,交
,交 的延长线于点
的延长线于点 ,如图
,如图
①请你在“思路一”中的括号内填写理由;
②根据“思路二”的提示,完整写出说明过程;
(2)如图3,若
 是等腰直角三角形,
是等腰直角三角形, ,点
,点 在线段
在线段 的延长线上,过点
的延长线上,过点 作
作 于
于 ,试探究
,试探究 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠APB=30°,OP=3cm,⊙O的半径为1cm,若圆心O沿着BP的方向在直线BP上移动.
(Ⅰ)当圆心O移动的距离为1cm时,则⊙O与直线PA的位置关系是 .
(Ⅱ)若圆心O的移动距离是d,当⊙O与直线PA相交时,则d的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个六边形的花坛被分割成7个部分,其中四边形PRBA,RQDC,QPFE为正方形。记正方形PRBA,RQDC,QPFE的面积分别为
 ,
, ,
, , RH⊥PQ,垂足为H。
, RH⊥PQ,垂足为H。(1)若PR⊥QR,
 =16,
=16, =9,则
=9,则 = ,RH= ;
= ,RH= ;(2)若四边形PRBA,RQDC,QPFE的面积分别为25m2、13m2、36m2

①求△PRQ的面积;
②请判断△PRQ和△DEQ的面积的数量关系,并证明你的结论;
③六边形花坛ABCDEF的面积是 m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=9,AB=CD=15.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长度

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).

相关试题

