【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=9,AB=CD=15.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长度

参考答案:
【答案】DE=3或27.
【解析】
分两种情况:点E在DC线段上,点E为DC延长线上的一点,进一步分析探讨得出答案即可.
如图1,
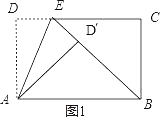
∵折叠,∴△AD′E≌△ADE,∴∠AD′E=∠D=90°,AD′=AD,
∵∠AD′B=90°,∴B、D′、E三点共线,
∵∠ABD′=∠BEC,∠AD′B=∠C=90°,AD′=BC,
∴ABD′≌△BEC,∴BE=AB=15,
∵BD′=![]() =
=![]() =12,
=12,
∴DE=D′E=15﹣12=3;
如图2,
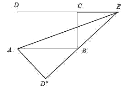
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
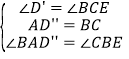 ,
,
∴△ABD″≌△BEC,
∴BE=AB=15,∴DE=D″E=15+12=27.
综上所知,DE=3或27.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠APB=30°,OP=3cm,⊙O的半径为1cm,若圆心O沿着BP的方向在直线BP上移动.
(Ⅰ)当圆心O移动的距离为1cm时,则⊙O与直线PA的位置关系是 .
(Ⅱ)若圆心O的移动距离是d,当⊙O与直线PA相交时,则d的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE。连结DC、BE交于F点。

(1)求证:△DAC≌△BAE;
(2)求证:DC⊥BE;
(3)求证:∠DFA=∠EFA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个六边形的花坛被分割成7个部分,其中四边形PRBA,RQDC,QPFE为正方形。记正方形PRBA,RQDC,QPFE的面积分别为
 ,
, ,
, , RH⊥PQ,垂足为H。
, RH⊥PQ,垂足为H。(1)若PR⊥QR,
 =16,
=16, =9,则
=9,则 = ,RH= ;
= ,RH= ;(2)若四边形PRBA,RQDC,QPFE的面积分别为25m2、13m2、36m2

①求△PRQ的面积;
②请判断△PRQ和△DEQ的面积的数量关系,并证明你的结论;
③六边形花坛ABCDEF的面积是 m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知顶点为(-3,-6)的抛物线
 经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程
经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程 的两根为﹣5和﹣1,其中正确的有( )
的两根为﹣5和﹣1,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
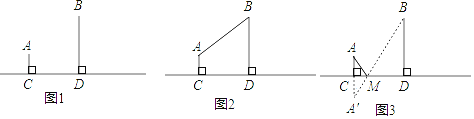
(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选
方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)
方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.
(2)有一艘快艇Q从这条河中驶过,当快艇Q在CD中间,DQ为多少时?△ABQ为等腰三角形?
相关试题

