【题目】如图(1)所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD.
(1)求证:EG=FG.
(2)若将△DEC的边EC沿AC方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

参考答案:
【答案】(1)证明见解析(2)成立
【解析】试题分析:(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFG≌△DEG,从而得出GE=GF;
(2)结论仍然成立,同理可以证明得到.
试题解析:(1)证明:∵DE⊥AC,BF⊥AC,
∴∠DEF=∠BFE=90°.
∵AE=CF,AE+EF=CF+EF.即AF=CE.
在Rt△ABF和Rt△CDE中, ![]() ,
,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△BFG和△DEG中, 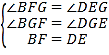 ,
,
∴△BFG≌△DGE(AAS),
∴GE=GF;
(2)结论依然成立.
理由:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°
∵AE=CF
∴AE﹣EF=CF﹣EF,即AF=CE,
在Rt△ABF和Rt△CDE中, ![]() ,
,
∴Rt△ABF≌Rt△CDE(HL),
∴DE=BF
在△BFG和△DEG中, 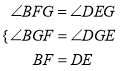 ,
,
∴△BFG≌△DGE(AAS),
∴GE=GF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC、∠BOA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查方式合适的是( )
A. 为了了解外地游客对岳阳楼新景区的感受,小华利用周日在汴河街随机采访了
 名武汉游客
名武汉游客B. 为了了解全校学生用于做数学作业的时间,小民同学在网上通过
 向
向 位好友做了调查
位好友做了调查C. 为了了解“嫦娥一号”卫星零部件的状况,检测人员采用了普查的方式
D. 为了了解全国青少年儿童在阳光体育运动启动后的睡眠时间,统计人员采用了普查的方式
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C.

(1)求A、B、C三点的坐标.
(2)求抛物线的对称轴及顶点坐标.
(3)抛物线上是否存在点F,使△ABF的面积为1?若存在,求F点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
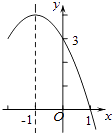
A.x=1
B.x=﹣1
C.x1=1,x2=﹣3
D.x1=1,x2=﹣4
相关试题

