【题目】如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C. 
(1)求A、B、C三点的坐标.
(2)求抛物线的对称轴及顶点坐标.
(3)抛物线上是否存在点F,使△ABF的面积为1?若存在,求F点的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵抛物线y=x2+4x+3交x轴于A、B两点,
∴令y=0,则x2+4x+3=0,
解得x1=﹣3、x2=﹣1,即点A(﹣3,0),B(﹣1,0),
令x=0,则y=3,
∴C(0,3)
(2)解:对称轴: ![]() =
= ![]() =﹣2;
=﹣2;
顶点坐标:x= ![]() =﹣2,y=
=﹣2,y= ![]() =
= ![]() =﹣1;
=﹣1;
顶点坐标为(﹣2,﹣1)
(3)解:∵A(﹣3,0),B(﹣1,0),
∴AB=2,
设F点坐标为(m,m2+4m+3),
则S△ABF= ![]() ×|m2+4m+3|=1,
×|m2+4m+3|=1,
∴|m2+4m+3|=1,
∴m2+4m+3=1或m2+4m+3=﹣1,
解得:m=﹣2+ ![]() 或m=﹣2﹣
或m=﹣2﹣ ![]() 或m=﹣2,
或m=﹣2,
∴点满足要求的点F的坐标为:(﹣2+ ![]() ,1)、(﹣2﹣
,1)、(﹣2﹣ ![]() ,1)、(﹣2,﹣1)
,1)、(﹣2,﹣1)
【解析】(1)根据x2+4x+3=0,解得x1=﹣3、x2=﹣1,即点A(﹣3,0),B(﹣1,0),根据抛物线y=x2+4x+3交y轴于点C,可知当x=0时,y=3,所以C(0,3);(2)根据二次函数y=ax2+bx+c的对称轴为x=﹣ ![]() ,顶点坐标为(
,顶点坐标为( ![]() ,
, ![]() ),求得抛物线的对称轴和顶点坐标;(3)设出F点的横坐标,纵坐标用横坐标表示,将三角形ABF的面积用F点的横坐标表示出来,等于1,建立方程,解之即可.
),求得抛物线的对称轴和顶点坐标;(3)设出F点的横坐标,纵坐标用横坐标表示,将三角形ABF的面积用F点的横坐标表示出来,等于1,建立方程,解之即可.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD.
(1)求证:EG=FG.
(2)若将△DEC的边EC沿AC方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查方式合适的是( )
A. 为了了解外地游客对岳阳楼新景区的感受,小华利用周日在汴河街随机采访了
 名武汉游客
名武汉游客B. 为了了解全校学生用于做数学作业的时间,小民同学在网上通过
 向
向 位好友做了调查
位好友做了调查C. 为了了解“嫦娥一号”卫星零部件的状况,检测人员采用了普查的方式
D. 为了了解全国青少年儿童在阳光体育运动启动后的睡眠时间,统计人员采用了普查的方式
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
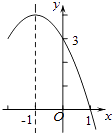
A.x=1
B.x=﹣1
C.x1=1,x2=﹣3
D.x1=1,x2=﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O上有两点A与P,且OA⊥OP,若A点固定不动,P点在圆上匀速运动一周,那么弦AP的长度d与时间t的函数关系的图象可能是( )


A.①
B.③
C.①或③
D.②或④ -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解参加某校运动会的
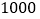 名运动员的年龄情况,从中抽取了
名运动员的年龄情况,从中抽取了 名运动员的年龄,就这个问题,下面说法正确的是( )
名运动员的年龄,就这个问题,下面说法正确的是( )A.
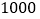 名运动员是总体 B. 每个运动员是个体
名运动员是总体 B. 每个运动员是个体C. 抽取的
 名运动员是样本 D. 每个运动员的年龄是个体
名运动员是样本 D. 每个运动员的年龄是个体
相关试题

