【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.

参考答案:
【答案】(1)y=-2x+340(20≤x≤40)(2)当x=40时,W最大,最大值为5200元
【解析】试题分析:(1)待定系数法求解可得;(2)根据:总利润=每千克利润×销售量,列出函数关系式,配方后根据x的取值范围可得W的最大值.
试题解析:(1)设y与x的函数关系式为y=kx+b,根据题意,得:![]() ,
,
解得:![]() , ∴y与x的函数解析式为y=﹣2x+340,(20≤x≤40).
, ∴y与x的函数解析式为y=﹣2x+340,(20≤x≤40).
(2)由已知得:W=(x﹣20)(﹣2x+340)=﹣2x2+380x﹣6800=﹣2(x﹣95)2+11250,
∵﹣2<0, ∴当x≤95时,W随x的增大而增大, ∵20≤x≤40,
∴当x=40时,W最大,最大值为﹣2(40﹣95)2+11250=5200元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,三边长a、b、c满足a2+8b2+c2-4b(a+c)=0,试判断△ABC的形状并加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据2,7,3,7,5,3,7的众数是( )
A. 2 B. 3 C. 5 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫作闭区间,表示为[a,b].对于任何一个二次函数,它在给定的闭区间上都有最小值.
(1)函数y=-x +4x-2在区间[0,5]上的最小值是________;
(2)求函数y=
 +
+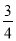 在区间
在区间 上的最小值.
上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据2,x,4,6的众数为4,则这组数据的平均数为( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据a1,a2,a3,a4的平均数是2017,则另一组数据a1+3,a2﹣2,a3﹣2,a4+5的平均数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
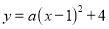 与
与 轴交于点A、B,与
轴交于点A、B,与 轴交于点C.过点C作CD//
轴交于点C.过点C作CD//  轴交抛物线的对称轴于点D,抛物线对称轴交x轴于点E,连接BD.已知点A的坐标为
轴交抛物线的对称轴于点D,抛物线对称轴交x轴于点E,连接BD.已知点A的坐标为 .
.(1)求抛物线的解析式;(2)求四边形COBD的面积.

相关试题

