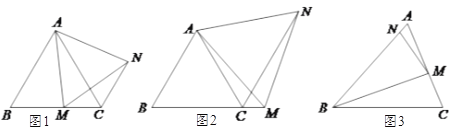
【题目】(Ⅰ)如图1,在等边![]() 中,点
中,点![]() 是
是![]() 上的任意一点(不含端点
上的任意一点(不含端点![]() ,
, ![]() ),连结
),连结![]() ,以
,以![]() 为边作等边
为边作等边![]() ,并连结
,并连结![]() .求证:
.求证: ![]() .
.
(Ⅱ)【类比探究】
如图2,在等边![]() 中,若点
中,若点![]() 是
是![]() 延长线上的任意一点(不含端点
延长线上的任意一点(不含端点![]() ),其它条件不变,则
),其它条件不变,则![]() 是否还成立?若成立,请说明理由;若不成立,请写出
是否还成立?若成立,请说明理由;若不成立,请写出![]() ,
, ![]() ,
, ![]() 三者间的数量关系,并给予证明.
三者间的数量关系,并给予证明.
(Ⅲ)【拓展延伸】
如图3,在等腰![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 上的任意一点(不含端点),连结
上的任意一点(不含端点),连结![]() ,以
,以![]() 为边作等腰
为边作等腰![]() ,使
,使![]() ,试探究
,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
参考答案:
【答案】(Ⅰ)证明见解析(Ⅱ)结论不成立(Ⅲ)![]()
【解析】试题分析:(Ⅰ)通过证明 ![]() ≌
≌![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() ,从而证得
,从而证得![]() ;
;
(Ⅱ)结论不成立,通过证明 ![]() ≌
≌![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() ,由
,由![]() ,得
,得![]() ;
;
(Ⅲ)![]() ,设
,设![]() ,由
,由![]() 为
为![]() 的外角,可得
的外角,可得![]() ,从而可得
,从而可得![]() ,又
,又![]() 为
为![]() 的外角,可得
的外角,可得![]() ,从而有
,从而有![]() ,继而推得
,继而推得![]() .
.
试题解析:(Ⅰ)∵![]() ,
, ![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() 即
即![]() ,
,
在![]() 和
和![]() 中,
中, 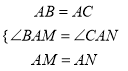 ,
,
![]()
![]() ≌
≌![]()
![]() ,
,
∴![]() ,
,
∴![]() ;
;
(Ⅱ)结论不成立,
理由: ![]() ,
, ![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() 即
即![]() ,
,
在![]() 和
和![]() 中,
中, 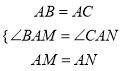 ,
,
![]()
![]() ≌
≌![]()
![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ;
;
(Ⅲ)![]() ,理由:
,理由:
设![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() 为
为![]() 的外角,
的外角,
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,
又![]() 为
为![]() 的外角,
的外角,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生? -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组)和不等式(组)
(1)
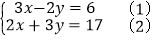 (2)
(2)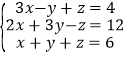
(3)
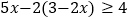 (4)
(4)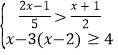
-
科目: 来源: 题型:
查看答案和解析>>【题目】服装店老板用45 000元购进一批羽绒服,由于深受顾客喜爱,很快售完.老板又用49 500元购进相同数量的该款羽绒服,但每件进价比第一批多了9元.根据题中信息,解答下列问题:
(Ⅰ)第一批羽绒服每件进价是多少元?
(Ⅱ)老板以每件120元的价格销售该款式羽绒服,当第二批羽绒服售出
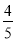 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于14 000元,则剩余的羽绒服每件售价至少要多少元?(利润
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于14 000元,则剩余的羽绒服每件售价至少要多少元?(利润 售价-进价)
售价-进价) -
科目: 来源: 题型:
查看答案和解析>>【题目】本学期开学前夕,某文具店用4000元购进若干书包,很快售完,接着又用4500元购进第二批书包,已知第二批所购进书包的只数是第一批所购进书包的只数的1.5倍,且每只书包的进价比第一批的进价少5元,求第一批书包每只的进价是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本,小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会表现突出的同学,要求笔记本数不少于钢笔数.请问:有多少购买方案?请你一一写出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年共享单车横空出世,更好地解决了人们“最后一公里”出行难的问题,截止到2016年底,已知“摩拜单车”投放数量有50万辆,“ofo共享单车”的投放数量是“摩拜单车”投放数量的1.6倍,“ofo共享单车”注册用户量比“摩拜单车”的注册用户量多210万人,据统计使用一辆“ofo共享单车”的平均人数比使用一辆“摩拜单车”的平均人数少3人,假设注册这两种单车的用户都在使用共享单车,求2016年“ofo共享单车”和“摩拜单车”的注册用户量各多少人?
相关试题

