【题目】如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为 . 
参考答案:
【答案】y= ![]() x
x
【解析】解:设直线l和10个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C, 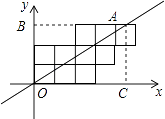
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这10个正方形分成面积相等的两部分,
∴两边分别是5,
∴三角形ABO面积是7,
∴ ![]() OBAB=7,
OBAB=7,
∴AB= ![]() ,
,
∴OC=AB= ![]() ,
,
由此可知直线l经过( ![]() ,3),
,3),
设直线方程为y=kx(k≠0),
则3= ![]() k,解得k=
k,解得k= ![]()
∴直线l解析式为y= ![]() x.
x.
故答案为:y= ![]() x.
x.
设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义{a,b,c}为函数y=ax2+bx+c的“特征数”.
(1)“特征数”为{﹣1,2,3}的函数解析式为 , 将“特征数”为{0,1,1}的函数向下平移两个单位以后得到的函数解析式为;
(2)我们把横、纵坐标均为整数的点称为“整点”,试问:在上述两空填写的函数图象围成的封闭图形(包含边界)内共有多少个整点?请给出详细的运算过程;
(3)定义“特征数”的运算:①{a1 , b1 , c1}+{a2 , b2 , c2}={a1+a2 , b1+b2 , c1+c2};②λ{a1 , b1 , c1}={λa1 , λb1 , λc1}(其中λ为任意常数).试问:“特征数”为{﹣1,2,3}+λ{0,1,﹣1}的函数是否过定点?如果过定点,请计算出该定点坐标;如果不存在,请说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,ABCD为正方形,直线MN分别过AD边与BC边的中点,点P为直线MN上任意一点,连接PB、PC分别与AD边交于E、F两点,PC与BD交于点K,连接AK与PB交于点G.
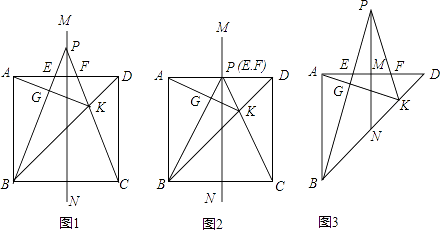
(1)探索发现
当点P落在AD边上时,如图2,试探究PB与AK的位置关系以及PB、PK、AK三者的数量关系(直接写出无需证明);
(2)延伸拓展
当点P落在正方形外,如图1,以上两个结论是否仍然成立?如果成立请给出证明,如果不成立请说明你的理由;
(3)应用推广
如图3,在等腰Rt△ABD中,其中∠BAD=90°,腰长为3,M、N分别为AD边与BD边的中点,K为线段DN中点,F为AD边上靠近于D的三等分点.连接KF并延长与直线MN交于点P,连接PB分别与AD、AK交于点E、G.试求四边形EFKG的周长及面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为 .

相关试题

