【题目】如图,点O是△ABC边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(Ⅰ)求证:OE=OF;
(Ⅱ)若CE=8,CF=6,求OC的长;
参考答案:
【答案】(Ⅰ)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6,
∵MN∥BC,
∴∠1=∠5,3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(Ⅱ)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF= ![]()
∴OC=EF=5;
【解析】(Ⅰ)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案; (Ⅱ)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有三层,第一层有商品(m+n)2种,第二层有商品m(m+n)种,第三层有商品n(m+n)种,求这个商场共有多少种商品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CE是△ABC外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G,求证:四边形ACGF是菱形.

-
科目: 来源: 题型:
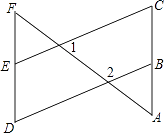
查看答案和解析>>【题目】如图,∠1=70°,∠2=110°,∠C=∠D,试探索∠A与∠F有怎样的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013 , 将等式两边同时乘2,
得2S=2+22+23+24+25+…+22013+22014 .
将下式减去上式,得2S﹣S=22014-1
即S=22014-1,
即1+2+22+23+24+…+22013=22014-1
仿照此法计算:
(1)1+3+32+33+…+3100
(2)1+ +…+
+…+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法按要求把2.0503分别取近似数,其中错误的是( )
A. 2.1(精确到0.1) B. 2.05(精确到0.001)
C. 2.05(精确到百分位) D. 2.050(精确到千分位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答

(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题: 如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
解:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: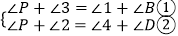
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P= (∠B+∠D)=26°.
(∠B+∠D)=26°.
①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
相关试题

