搜索
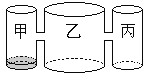
【题目】实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1：2：1，，用两个相同的管子在容器的5cm高度处连通（即管子底端离容器底5cm），现三个容器中，只有甲中有水，水位高1cm，如图所示．若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升
cm，则开始注入 分钟的水量后，甲与乙的水位高度之差是0．5cm．
参考答案：
【答案】
，
，
【解析】
试题∵甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1:2:1，∴甲、乙、丙三个圆柱形容器的底面积之比为1：4：1，∵每分钟同时向乙和丙注入相同量的水，注水1分钟，乙的水位上升
cm，∴注水1分钟，丙的水位上升
cm，
当甲比乙高0．5cm时，此时乙中水位高0．5cm，用时0．5÷=分；
当丙的高度到5cm时，此时用时为5÷
=
分，此时乙中水高
=
<1+0．5，在这之后丙中的水流入乙中，乙每分钟水位上升
cm，1．5-=
，
分，即开始注水后乙比甲高0．5cm的用时为
分；
当乙的水位达到5cm时开始流向甲，此时用时为
=
分，甲水位每分上升
cm，当甲的水位高为4．5cm时，乙比甲高0．5cm，此时用时
=分；
综上，开始注入
分钟的水量后，甲与乙的水位高度之差是0．5cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实根，且其中一个根为另一根的2倍，则称这样的方程为“倍根方”，以下关于倍根方程的说法正确的是______（填正确序号）
①方程x2﹣x﹣2=0是倍根方程．
②若（x﹣2）（mx+n）=0是倍根方程，则4m2+5mn+n2=0．
③若点（p，q）在反比例函数y=
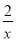的图象上，则关于x的方程px2+3x+q=0是倍根方程．④若方程ax2+bx+c=0是倍根方程且相异两点M（1+t，s）、N（4﹣t，s）都在抛物线y=ax2+bx+c上，则方程ax2+bx+c=0必有一个根为
． -
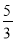科目： 来源： 题型：
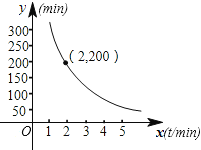
查看答案和解析>>【题目】码头工人往一艘轮船上装载货物，装完货物所需时间
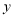
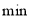与装载速度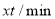
之间的函数关系如图.（1）这批货物的质量是多少?并求出
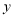与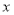
之间的函数关系式；（2）轮船到达目的地后开始卸货，如果以5t/min的速度卸货，那么需要多少小时才能卸完货？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG.
(1)求证：△ABG≌△AFG；(2)求BG的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：
（1）在这项调查中，共调查了多少名学生？
（2）请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；
（3）若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
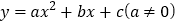与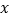
轴交于A、B两点，与y轴交于点C（0，3），且此抛物线的顶点坐标为M（-1，4）.（1）求此抛物线的解析式；
（2）设点D为已知抛物线对称轴上的任意一点，当△ACD面积等于6时，求点D的坐标；
（3）点P在线段AM上，当PC与y轴垂直时，过点P作
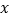轴的垂线，垂足为E，将△PCE沿直线CB翻折，使点P的对应点P'与P、E、C处在同一平面内，请求出P'坐标，并判断点P'是否在抛物线上.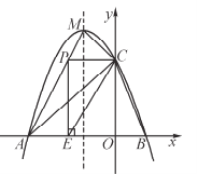
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，已知AB=4，BC=3，矩形在直线
上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图②位置，...，以此类推，这样连续旋转2018次后，顶点A在整个旋转过程中所经过的路程之和是____________．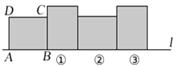
相关试题
