【题目】如图,抛物线![]() 与
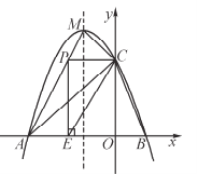
与![]() 轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
(1)求此抛物线的解析式;
(2)设点D为已知抛物线对称轴上的任意一点,当△ACD面积等于6时,求点D的坐标;
(3)点P在线段AM上,当PC与y轴垂直时,过点P作![]() 轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
参考答案:
【答案】(1) ![]() ;M(-1,4);(2)点D的坐标为(-1,-2)或(-1,6).
;M(-1,4);(2)点D的坐标为(-1,-2)或(-1,6).
;(3)点P′不在该抛物线上.
【解析】分析:(1)由抛物线经过的C点坐标以及顶点M的坐标,利用待定系数法即可求出抛物线解析式;
(2)设点D坐标为(﹣1,yD),根据△ACD的面积=6,即可得出关于yD含绝对值符号的一元一次方程,解方程即可得出结论;
(3)作点P关于直线CE的对称点P′,过点P′作PH⊥y轴于H,设P′E交y轴于点N.根据对称的性质即可得出△EON≌△CP′N,从而得出CN=NE,由点A、M的坐标利用待定系数法可求出直线AM的解析式,进而得出点P的坐标.在Rt△P′NC中,由勾股定理可求出CN的值,再由相似三角形的性质以及线段间的关系即可找出点P′的坐标,将其代入抛物线解析式中看等式是否成立,由此即可得出结论.
详解:(1)∵抛物线y=ax2+bx+c经过点C(0,3),顶点为M(﹣1,4),∴ ,解得:
,解得: ,∴所求抛物线的解析式为y=﹣x2﹣2x+3.
,∴所求抛物线的解析式为y=﹣x2﹣2x+3.
(2)依照题意画出图形,如图1所示.
令y=﹣x2﹣2x+3=0,解得:x=﹣3或x=1,故A(﹣3,0),B(1,0),∴OA=OC,△AOC为等腰直角三角形.
设AC交对称轴x=﹣1于F(﹣1,yF),由点A(﹣3,0)、C(0,3)可知直线AC的解析式为y=x+3,∴yF=﹣1+3=2,即F(﹣1,2).
设点D坐标为(﹣1,yD),则S△ADC=![]() DFAO=
DFAO=![]() ×|yD﹣2|×3=6.
×|yD﹣2|×3=6.
解得:yD=﹣2或yD=6,∴点D的坐标为(﹣1,﹣2)或(﹣1,6).
(3)如图2,点P′为点P关于直线CE的对称点,过点P′作PH⊥y轴于H,设P′E交y轴于点N.
在△EON和△CP′N中,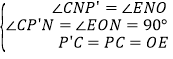 ,∴△EON≌△CP′N(AAS).
,∴△EON≌△CP′N(AAS).
设NC=m,则NE=m.
∵A(﹣3,0)、M(﹣1,4)可知直线AM的解析式为y=2x+6,∴当y=3时,x=﹣![]() ,即点P(﹣
,即点P(﹣![]() ,3),∴P′C=PC=
,3),∴P′C=PC=![]() ,P′N=3﹣m.在Rt△P′NC中,由勾股定理,得:
,P′N=3﹣m.在Rt△P′NC中,由勾股定理,得:![]() +(3﹣m)2=m2,解得:m=
+(3﹣m)2=m2,解得:m=![]() .
.
∵S△P′NC=![]() CNP′H=
CNP′H=![]() P′NP′C,∴P′H=
P′NP′C,∴P′H=![]() .
.
由△CHP′∽△CP′N可得:![]() ,∴CH=
,∴CH=![]() =
=![]() ,∴OH=3﹣
,∴OH=3﹣![]() =
=![]() ,∴P′的坐标为(
,∴P′的坐标为(![]() ).
).
将点P′(![]() )代入抛物线解析式,得:y=﹣
)代入抛物线解析式,得:y=﹣![]() ﹣2×
﹣2×![]() +3=
+3=![]() ≠
≠![]() ,∴点P′不在该抛物线上.
,∴点P′不在该抛物线上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升
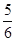 cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.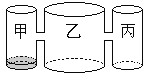
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线
 上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,...,以此类推,这样连续旋转2018次后,顶点A在整个旋转过程中所经过的路程之和是____________.
上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,...,以此类推,这样连续旋转2018次后,顶点A在整个旋转过程中所经过的路程之和是____________.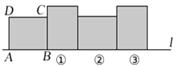
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按如图方式拼图,第1个图形共用3根火柴棒,第2个图形共用9根火柴棒,第3个图形共用18根火柴棒,……按照这样的方式继续拼图,第n个图形共用_____根火柴棒.(用含n的代数式表示)

-
科目: 来源: 题型:
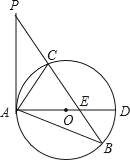
查看答案和解析>>【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AGAB=12,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.
相关试题

