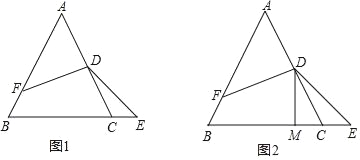
【题目】如图1,等边△ABC中,D为AC中点,∠EDF=120°,DF交AB于F点,且AF=nBF(n为常数,且n>1).
(1)求证:DF=DE;
(2)如图1,求证:AF﹣CE=![]() AB;
AB;
(3)如图2,当n= 时,过D作DM⊥BC于M点,C为EM的中点.
参考答案:
【答案】(1)见解析;(2)见解析;(3)3.
【解析】
(1)过D点作DG∥BC交AB于G点,证明△DGF≌△DCE,根据全等三角形的性质证明即可;
(2)根据全等三角形的性质得到GF=CE,结合图形证明;
(3)根据直角三角形的性质得到CM=![]() CD,得到GF=
CD,得到GF=![]() AG,根据等边三角形的性质解答.
AG,根据等边三角形的性质解答.
解:(1)证明:过D点作DG∥BC交AB于G点,
∵DG∥BC,
∴∠ADG=∠ACB=60°=∠A,
∴△AGD为等边三角形,
∴GD=AD=DC,
∵∠GDC=∠FDE=120°,
∴∠GDF=∠DCE,
在△DGF和△DCE中,
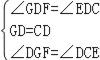
∴△DGF≌△DCE(ASA)
∴DF=DE;
(2)∵△DGF≌△DCE,
∴GF=CE,
∵DG∥BC,D为AC中点,
∴AG=![]() AB,
AB,
∴AF﹣CE=AF﹣GF=AG=![]() AB;
AB;
(3)∵DM⊥BC,∠DCM=60°,
∴CM=![]() CD,
CD,
∵C为EM的中点,
∴CE=![]() CD,
CD,
由(1)得,CE=GF,
∴GF=![]() CD,
CD,
∴GF=![]() AG=
AG=![]() GB,
GB,
∴AF=3BF,
∴n=3,
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑车从家出发,先向东骑行1km到达A村,继续向东骑行4km到达B村,然后向西骑行8km到达C村,最后回到家.
(1) 以快递公司为原点,以向东方向为正方向,用1 cm表示1 km,画出数轴,并在数轴上表示出A、B、C三个店的位置;
(2) C店离A店有多远?
(3) 快递员一共骑行了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】快车和慢车同时从甲、乙两地出发开往乙地和甲地,匀速行驶,快车到达乙地后休息一个小时按原速返回,慢车在快车前一个小时到达甲地.如图表示慢车行驶过程中离甲地的路程y(km)与出发时间x(h)的函数图象,请结合图中的信息,解答下列问题:

(1)甲、乙两地的距离为 km,慢车的速度为 km/h,快车的速度为 km/h;
(2)在图①中画出快车离甲地的路程y(km)与出发时间x(h)的函数图象(坐标轴标注相关数值);
(3)求出发多长时间,两车相距150km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组同学在一周内阅读课外科普读物与人数情况如表所示:
课外科普读物(本数)
4
5
6
人数
3
2
1
下列关于“课外科普读物”这组数据叙述正确的是
A.中位数是3
B.众数是4
C.平均数是5
D.方差是6 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市准备将一批帐篷和食品送往扶贫区.已知帐篷和食品共320件,且帐篷比食品多80件.
(1)直接写出帐篷有 件,食品有 件;
(2)现计划租用A、B两种货车共8辆,一次性将这批物资全部送到扶贫区,已知两种车可装帐篷和食品的件数以及每辆货车所需付运费情况如表,问:共有几种租车的方案?最少运费是多少?
帐篷(件)
食品(件)
每辆需付运费(元)
A种货车
40
10
780
B种货车
20
20
700
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.
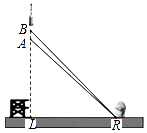
(1)求发射台与雷达站之间的距离LR;
(2)求这枚火箭从A到B的平均速度是多少?(结果精确到0.01,参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02 ) -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
相关试题

