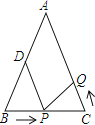
【题目】如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.
(1)若点P的速度为3cm/s,用含t的式子表示第t秒时,BP= cm,CP= cm.
(2)在(1)的条件下,若点Q运动速度与点P的运动速度相等,经过几秒钟△BPD与△CQP全等,说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,且点P的速度比点Q的速度慢1cm/s时,点Q的运动速度为多少时?能够使△BPD与△CQP全等?
参考答案:
【答案】(1)3t,8﹣3t;(2)经过1秒钟△BPD与△CQP全等,见解析;(3)Q的速度是5cm/s时,△BPD≌△CQP
【解析】
(1)根据路程=速度×时间就可以得出结论;
(2)当BP=PC时,BD=CQ,由BP+CP=BC=8,得出BP=4,t=![]() s CQ=4不成立;
s CQ=4不成立;
当BP=CQ时,BD=CP,由中点的定义得出BD=AD=5,CP=5,BP=3,即可得出结果;
(3)设Q的速度为acm/s,则P的速度为(a﹣1)cm/s,由BP与CQ不相等,得出BD=CQ,BP=CP,设运动时间为ts,则at=5,(a﹣1)t=4,解得t=1s,a=5cm/s即可.
解:(1)∵由题意得:BP=3t,
∴PC=8﹣3t;
故答案为:3t,8﹣3t;
(2)经过1秒钟△BPD与△CQP全等,理由如下:
当BP=PC时,BD=CQ,
∵BP+CP=BC=8,
∴BP=4,
∴t=![]() s CQ=4不成立;
s CQ=4不成立;
当BP=CQ时,BD=CP,
∵点D为AB的中点,
∴BD=AD,
∵AB=10,
∴BD=5,
∴CP=5,
∴BP=3,
∴t=1,故t=1;
即若点Q运动速度与点P的运动速度相等,经过1秒钟△BPD与△CQP全等;
(3)设Q的速度为acm/s,则P的速度为(a﹣1)cm/s,
∵BP与CQ不相等,
∴BD=CQ,BP=CP,
设运动时间为ts,
∴at=5,(a﹣1)t=4,
∴t=1s,a=5cm/s;
即Q的速度是5cm/s时,△BPD≌△CQP.
-
科目: 来源: 题型:
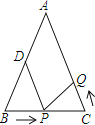
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将2×2的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )

A.3
B.2
C.1
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )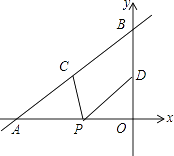
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ,0)
,0)
D.(﹣ ,0)
,0) -
科目: 来源: 题型:
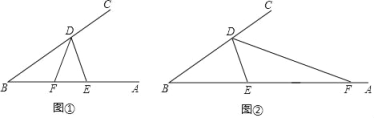
查看答案和解析>>【题目】已知点D、E分别是∠B的两边BC、BA上的点,∠DEB=2∠B,F为BA上一点.
(1)如图①,若DF平分∠BDE,求证:BD=DE+EF;
(2)如图②,若DF为△DBE的外角平分线,BD、DE、EF三者有怎样的数量关系?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试说明CD⊥AB.

解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义).
∴DG∥AC(__________________).
∴∠2=∠________(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠________(等量代换).
∴EF∥CD(__________________).
∴∠AEF=∠________ (__________________).
∵EF⊥AB(已知).
∴∠AEF=90°(__________________).
∴∠ADC=90°(__________________).
∴CD⊥AB(__________________).
-
科目: 来源: 题型:
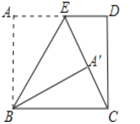
查看答案和解析>>【题目】如图,矩形
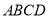 中,
中,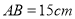 ,点
,点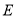 在
在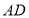 上,且
上,且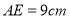 ,连接
,连接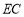 ,将矩形
,将矩形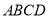 沿直线
沿直线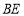 翻折,点
翻折,点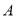 恰好落在
恰好落在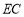 上的点
上的点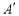 处,则
处,则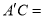 ________
________ .
.
A.9B.8C.7D.5
相关试题

