【题目】(9分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试说明CD⊥AB.

解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义).
∴DG∥AC(__________________).
∴∠2=∠________(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠________(等量代换).
∴EF∥CD(__________________).
∴∠AEF=∠________ (__________________).
∵EF⊥AB(已知).
∴∠AEF=90°(__________________).
∴∠ADC=90°(__________________).
∴CD⊥AB(__________________).
参考答案:
【答案】解:同位角相等,两直线平行;ACD;ACD;同位角相等,两直线平行;ADC,两直线平行,同位角相等;垂直定义;等量代换;垂直定义.
【解析】试题分析:由DG⊥BC,AC⊥BC,则可得∠DGB=∠ACB=90°,根据平行线的判定定理可得DG∥AC;接下来根据平行线的性质可得:∠2=∠DCA,结合∠1=∠2可得到:∠1=∠DCA,继而推出CD∥EF;接下来根据EF⊥AB,CD∥EF,可得到CD与AB的位置关系.
解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直定义).
∴DG∥AC(同位角相等,两直线平行).
∴∠2=∠ACD (两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠ACD (等量代换).
∴EF∥CD(同位角相等,两直线平行).
∴∠AEF=∠ADC, (两直线平行,同位角相等).
∵EF⊥AB(已知).
∴∠AEF=90°(垂直定义).
∴∠ADC=90°(等量代换).
∴CD⊥AB(垂直定义).
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣3x=0解为( )
A.x=0B.x=3C.x=0或x=3D.x=0且x=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在△ABC中,点O是∠ABC和∠ACB的平分线的交点,若∠A=α,则∠BOC=90°+
 ;如图②,∠CBO=
;如图②,∠CBO=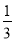 ∠ABC,∠BCO=
∠ABC,∠BCO= ∠ACB,∠A=α,则∠BOC=__________(用α表示);
∠ACB,∠A=α,则∠BOC=__________(用α表示);(2)如图③,∠CBO=
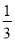 ∠DBC,∠BCO=
∠DBC,∠BCO= ∠ECB,∠A=α,请猜想∠BOC=__________(用α表示).
∠ECB,∠A=α,请猜想∠BOC=__________(用α表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.直径是弦,弦是直径
B.圆有无数条对称轴
C.无论过圆内哪一点,都只能作一条直径
D.度数相等的弧是等弧
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运输公司用10辆相同的汽车将一批苹果运到外地,每辆汽车能装8吨甲种苹果,或10吨乙种苹果,或11吨丙种苹果.公司规定每辆车只能装同一种苹果,而且必须满载.已知公司运送了甲、乙、丙三种苹果共100吨,且每种苹果不少于一车.
(1)设用x辆车装甲种苹果,y辆车装乙种苹果,求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若运送三种苹果所获利润的情况如下表所示:

设此次运输的利润为W(万元),问:如何安排车辆分配方案才能使运输利润W最大,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=500,∠C=600,求∠DAE和∠BOA的度数。

相关试题

