【题目】如图,已知函数![]() 的图象为直线
的图象为直线![]() ,函数
,函数![]() 的图象为直线
的图象为直线![]() ,直线
,直线![]() 、
、![]() 分别交
分别交![]() 轴于点
轴于点![]() 和点
和点![]() ,分别交
,分别交![]() 轴于点
轴于点![]() 和
和![]() ,
,![]() 和
和![]() 相交于点
相交于点![]()
(1)填空:![]() ;求直线
;求直线![]() 的解析式为 ;
的解析式为 ;
(2)若点![]() 是
是![]() 轴上一点,连接
轴上一点,连接![]() ,当
,当![]() 的面积是
的面积是![]() 面积的2倍时,请求出符合条件的点
面积的2倍时,请求出符合条件的点![]() 的坐标;
的坐标;
(3)若函数![]() 的图象是直线
的图象是直线![]() ,且
,且![]() 、
、![]() 、
、![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.

参考答案:
【答案】(1)![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() 或
或![]() ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将点![]() 坐标代入
坐标代入![]() 中,即可得出结论;将点
中,即可得出结论;将点![]() ,
,![]() 坐标代入
坐标代入![]() 中,即可得出结论;
中,即可得出结论;
(2)先利用两三角形面积关系判断出![]() ,再分两种情况,即可得出结论;
,再分两种情况,即可得出结论;
(3)分三种情况,利用两直线平行,![]() 相等或经过点
相等或经过点![]() 讨论即可得出结论.
讨论即可得出结论.
解:(1)![]() 点
点![]() 在函数
在函数![]() 的图象上,
的图象上,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 过点
过点![]() 、
、![]() ,
,
可得方程组为![]() ,
,
解得![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
故答案为:![]() ;
;![]()
(2)![]() 是
是![]() 与
与![]() 轴的交点,当
轴的交点,当![]() 时,
时,![]() ,
,
![]() ,
,![]() 坐标为
坐标为![]() ,
,
又![]() 的面积是
的面积是![]() 面积的2倍,
面积的2倍,
![]()
第一种情况,当![]() 在线段
在线段![]() 上时,
上时,
![]() ,
,
![]() ,即
,即![]() ,
,
∴![]() ,
,
![]() 坐标
坐标![]() ,
,
第二种情况,当![]() 在射线
在射线![]() 上时,
上时,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 坐标
坐标![]() ,
,
![]() 点的坐标为
点的坐标为![]() 或
或![]() ;
;
(3)![]() 、
、![]() 、
、![]() 不能围成三角形,
不能围成三角形,
![]() 直线
直线![]() 经过点
经过点![]() 或
或![]() 或
或![]() ,
,
①![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入到解析式中得:
代入到解析式中得:
![]() ,
,
![]() ,
,
②当![]() 时,
时,
∵直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
③当![]() 时,
时,
∵直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
即![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:求代数式x2+4x+8的最小值.
解:因为x2+4x+8=(x2+4x+4)+4=(x+2)2+4≥4,所以当x=﹣2时,代数式x2+4x+8有最小值,最小值是4.仿照上述解题过程求值.
(1)应用:求代数式m2+2m+3的最小值.
(2)拓展:求代数式﹣m2+3m+
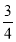 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为C(a,0),点C的坐标为(0,b),且a,b满足(a﹣4)2+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→C→B→A→O的路线移动.
(1)a= ,b= ,点B的坐标为 .
(2)当点P移动4秒时,请说明点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为
 ,所以这个三角形是常态三角形.
,所以这个三角形是常态三角形.(1)若
 三边长分别是2,
三边长分别是2, 和4,则此三角形 常态三角形(填“是”或“不是”
和4,则此三角形 常态三角形(填“是”或“不是”  ;
;(2)如图,
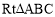 中,
中, ,
, ,点
,点 为
为 的中点,连接
的中点,连接 ,若
,若 是常态三角形,求
是常态三角形,求 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有( )

A. 3个B. 4个C. 5个D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
(1)若∠B=50°,∠C=30°,则∠DAE= .
(2)若∠B=60°,∠C=20°,则∠DAE= .
(3)由(1)(2)猜想∠DAE与∠B,∠C之间的关系为 ,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )

A. 4 B.
 C.
C.  D.
D. 
相关试题

