【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E. 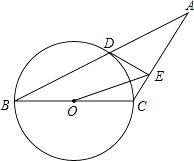
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积. 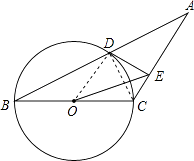
参考答案:
【答案】
(1)证明:连接OD,CD,

∵BC为⊙O直径,
∴∠BDC=90°,
即CD⊥AB,
∵△ABC是等腰三角形,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵D点在⊙O上,
∴DE为⊙O的切线;
(2)解:∵∠A=∠B=30°,BC=4,
∴CD= ![]() BC=2,BD=BCcos30°=2
BC=2,BD=BCcos30°=2 ![]() ,
,
∴AD=BD=2 ![]() ,AB=2BD=4
,AB=2BD=4 ![]() ,
,
∴S△ABC= ![]() ABCD=
ABCD= ![]() ×4
×4 ![]() ×2=4
×2=4 ![]() ,
,
∵DE⊥AC,
∴DE= ![]() AD=
AD= ![]() ×2
×2 ![]() =
= ![]() ,
,
AE=ADcos30°=3,
∴S△ODE= ![]() ODDE=
ODDE= ![]() ×2×
×2× ![]() =
= ![]() ,
,
S△ADE= ![]() AEDE=
AEDE= ![]() ×
× ![]() ×3=
×3= ![]() ,
,
∵S△BOD= ![]() S△BCD=
S△BCD= ![]() ×
× ![]() S△ABC=
S△ABC= ×4
![]() =
= ![]() ,
,
∴S△OEC=S△ABC﹣S△BOD﹣S△ODE﹣S△ADE=4 ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)首先连接OD,CD,由以BC为直径的⊙O,可得CD⊥AB,又由等腰三角形ABC的底角为30°,可得AD=BD,即可证得OD∥AC,继而可证得结论;(2)首先根据三角函数的性质,求得BD,DE,AE的长,然后求得△BOD,△ODE,△ADE以及△ABC的面积,继而求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解市民“获取新闻的最主要途径”某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
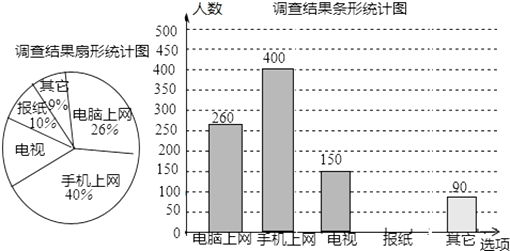
根据以上信息解答下列问题:
(1)这次接受调查的市民总人数是;
(2)扇形统计图中,“电视”所对应的圆心角的度数是;
(3)请补全条形统计图;
(4)若该市约有80万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象相交于点A(1,5)和点B,与y轴相交于点C(0,6).
的图象相交于点A(1,5)和点B,与y轴相交于点C(0,6). 
(1)求一次函数和反比例函数的解析式;
(2)现有一直线l与直线y=kx+b平行,且与反比例函数y= 的图象在第一象限有且只有一个交点,求直线l的函数解析式.
的图象在第一象限有且只有一个交点,求直线l的函数解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
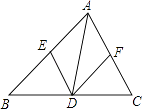
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.

(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为4cm,直线l与⊙O相交于A、B两点,AB=4
 cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 .
cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 . 
相关试题

