【题目】如图,⊙O的半径为4cm,直线l与⊙O相交于A、B两点,AB=4 ![]() cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 .
cm,P为直线l上一动点,以1cm为半径的⊙P与⊙O没有公共点.设PO=dcm,则d的范围是 . 
参考答案:
【答案】d>5或2≤d<3
【解析】解:连接OP、OA, ∵⊙O的半径为4cm,1cm为半径的⊙P,⊙P与⊙O没有公共点,
∴d>5时,两圆外离,
当两圆内切时,过点O作OD⊥AB于点D,
OP′=4﹣1=3cm,OD= ![]() =2(cm),
=2(cm),
∴以1cm为半径的⊙P与⊙O没有公共点时,2≤d<3,
所以答案是:d>5或2≤d<3.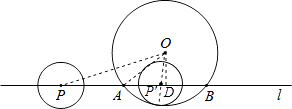
【考点精析】本题主要考查了圆与圆的位置关系的相关知识点,需要掌握两圆之间有五种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交.两圆圆心之间的距离叫做圆心距.两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
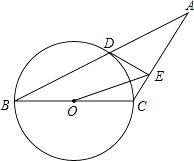
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.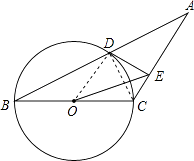
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.

(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:( )﹣1+|3tan30°﹣1|﹣(π﹣3)0;
)﹣1+|3tan30°﹣1|﹣(π﹣3)0;
(2)先化简,再求值:
 ,其中x=
,其中x=  ﹣3.
﹣3. -
科目: 来源: 题型:
查看答案和解析>>【题目】保障房建设是民心工程,某市从2008年开始加快保障房建设进程,现统计了该市2008年到2012年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.

(1)小丽看了统计图后说:“该市2011年新建保障房的套数比2010年少了.”你认为小丽说法正确吗?请说明理由;
(2)求补全条形统计图;
(3)求这5年平均每年新建保障房的套数. -
科目: 来源: 题型:
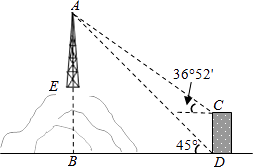
查看答案和解析>>【题目】如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
相关试题

