【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y=![]() (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为![]() .
.
(1)求k和m的值;
(2)求当x≥1时函数值y的取值范围.

参考答案:
【答案】(1)m=![]() ,k=1;(2)当x≥1时,y的取值范围为0<y≤1.
,k=1;(2)当x≥1时,y的取值范围为0<y≤1.
【解析】试题分析:(1)根据三角形的面积公式先得到m的值,然后把点A的坐标代入y=![]() ,可求出k的值;
,可求出k的值;
(2)求出x=1时,y的值,再根据反比例函数的性质求解.
试题解析:(1)∵A(2,m),∴OB=2,AB=m,∴S△AOB=![]() OBAB=
OBAB=![]() ×2×m=
×2×m=![]() ,
,
∴m=![]() ,∴点A的坐标为(2,
,∴点A的坐标为(2, ![]() ),
),
把A(2, ![]() )代入y=
)代入y=![]() ,得k=1;
,得k=1;
(2)∵当x=1时,y=1,
又∵反比例函数y=![]() 在x>0时,y随x的增大而减小,
在x>0时,y随x的增大而减小,
∴当x≥1时,y的取值范围为0<y≤1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+6与x轴、y轴分别相交于点E,F,点E的坐标为(8,0),点A的坐标为(6,0),点P(x,y)是第一象限内直线上的一个动点(点P不与点E,F重合).
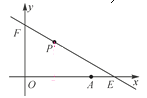
(1)求k的值;
(2)在点P运动的过程中,求出△OPA的面积S与x的函数关系式;
(3)若△OPA的面积为
 ,求此时点P的坐标.
,求此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(4,0),点P是第一象限内直线y=-x+6上一点.O是坐标原点.
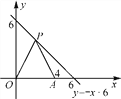
(1)设P(x,y),求△OPA的面积S与x的函数解析式;
(2)当S=10时,求P点的坐标;
(3)在直线y=-x+6上求一点P,使△POA是以OA为底边的等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4y2的结果是( )
A.(x+4y)(x﹣4y)
B.(x+2y)(x﹣2y)
C.(x﹣4y)2
D.(x﹣2y)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级各班分别选出3名学生组成班级代表队,参加知识竞赛,得分最多的班级为优胜班级,各代表队比赛结果如下:
班级
七(1)
七(2)
七(3)
七(4)
七(5)
七(6)
七(7)
七(8)
七(9)
七(10)
得分
85
90
90
100
80
100
90
80
85
90
(1)写出表格中得分的众数、中位数;
(2)学校从获胜班级的代表队中各抽取1名学生组成“绿色环保监督”小组,小明、小红分别是七(4)班和七(6)班代表队的学生,用列表法或画树状图的方法说明同时抽到小明和小红的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a-1|+|b+2|+|3c-6|=0,比较a,b,c的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式运算正确的是( )
A.3x+3y=6xy
B.7x﹣5x=2x2
C.16y2﹣7y2=9
D.19a2b﹣9ba2=10a2b
相关试题

