【题目】已知[x]表示不超过x的最大整数,如[3]=3;[3.14]=3;[﹣3.14]=﹣4.
根据以上规则解答下列问题:
(1)[﹣8]= ;[5.4]= ;[﹣6.99]= ;
(2)若[x]=﹣5,则x的范围是 ;
(3)已知正整数n小于100,![]() =n﹣2,求所有满足条件正整数n.
=n﹣2,求所有满足条件正整数n.
参考答案:
【答案】(1)-8;5;﹣7;(2)﹣5≤x<﹣4;(3)5,11,17.
【解析】
(1)根据[x]的定义即可求解;
(2)根据[x]的定义即可求解;
(3)首先根据正整数n小于100,确定![]() ]的范围,从而确定n的值的范围,然后进行排除即可.
]的范围,从而确定n的值的范围,然后进行排除即可.
(1)[﹣8]=﹣8;[5.4]=5;[﹣6.99]=﹣7;
(2)若[x]=﹣5,则x的范围是﹣5≤x<﹣4;
(3)∵正整数n小于100,
∴0<[![]() ]<50,
]<50,
0<[![]() ]≤33,
]≤33,
0<[![]() ]≤16,
]≤16,
又∵n﹣2≥0,
∴0≤n﹣2≤16,
∴2≤n≤18.
则在这个范围内满足条件的正整数有:5,11,17.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具
途中平均速度(千米/时)
运费(元/千米)
装卸费用(元)
火车
100
15
2000
汽车
80
20
900
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(3a2-ab+7)-(5ab-4a2+7),其中, a=2,b=
 ;
;(2)3(ab-5b2+2a2)-(7ab+16a2-25b2),其中|a-1|+(b+1)2=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图1),然后拼成一个平行四边形(如图2)。那么通过计算两个图形的阴影部分的面积,可以验证成立的公式是( )
A.a2-b2=(a-b)2
B.(a+b)2="a+2ab+b"
C.(a-b)2=a2-2ab+b2
D.a2-b2=(a-b)(a+b)

-
科目: 来源: 题型:
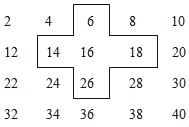
查看答案和解析>>【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2,4,6,8,…,排成如表,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)设中间的数为x,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,其他五个数的和能等于2 016吗?如能,写出这五个数,如不能,说明理由.
相关试题

