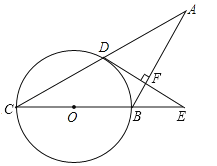
【题目】如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,tanC=![]() ,求EF的长.
,求EF的长.
参考答案:
【答案】(1)直线DE是⊙O的切线;(2)![]() .
.
【解析】试题分析:(1)连接圆心和切点,利用平行,OF⊥CB可证得∠ODF=90°;
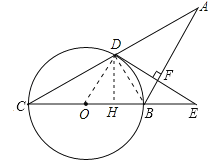
(2)过D作DH⊥BC于H,设BD=k,CD=2k,求得BD、CD的长,根据三角形的面积公式得到DH的长,由勾股定理得到OH的长,根据射影定理得到OD2=OHOE,求得OE的长,从而得到BE的长,根据相似三角形的性质得到BF=2,根据勾股定理即可得到结论.
试题解析:解:(1)证明:如图,连接OD,BD,∵AB是⊙O的直径,∴∠ADB=∠90°,∴BD⊥AC.
∵AB=BC,∴AD=DC.∵OA=OB,∴OD∥BC,∵DE⊥BC,∴DE⊥OD,∴直线DE是⊙O的切线.
(2)过D作DH⊥BC于H,∵⊙O的半径R=5,tanC=![]() ,∴BC=10,设BD=k,CD=2k,∴BC=
,∴BC=10,设BD=k,CD=2k,∴BC=![]() k=10,∴k=2
k=10,∴k=2![]() ,∴BD=2
,∴BD=2![]() ,CD=4
,CD=4![]() ,∴DH=
,∴DH=![]() =4,∴OH=
=4,∴OH=![]() =3,∵DE⊥OD,DH⊥OE,∴OD2=OHOE,∴OE=
=3,∵DE⊥OD,DH⊥OE,∴OD2=OHOE,∴OE=![]() ,∴BE=
,∴BE=![]() ,∵DE⊥AB,∴BF∥OD,∴△BFE∽△ODE,∴
,∵DE⊥AB,∴BF∥OD,∴△BFE∽△ODE,∴![]() ,即
,即 ,∴BF=2,∴EF=
,∴BF=2,∴EF=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)ax4﹣ay4
(2)﹣4x2+12xy﹣9y2.
-
科目: 来源: 题型:
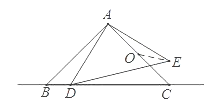
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
A.
 B.
B. C.1 D.
C.1 D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填注理由:
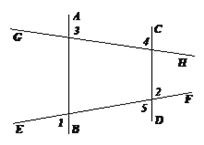
如图,已知:直线AB,CD被直线EF,GH所截,且∠1=∠2,
试说明:∠3+∠4=180°.
解:∵∠1=∠2 (______________)
又∵∠2=∠5 (________)
∴∠1=∠5 (________)
∴AB∥CD (________)
∴∠3+∠4=180(________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】 下列命题的逆命题为真命题的是( )
A.对顶角相等B.内错角相等,两直线平行
C.直角都相等D.如果x=3,那么|x|=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2;再向正东方向走6m到达点A3;再向正南方向走8m到达点A4;再向正西方向走10m到达点A5;…,按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为________.

-
科目: 来源: 题型:
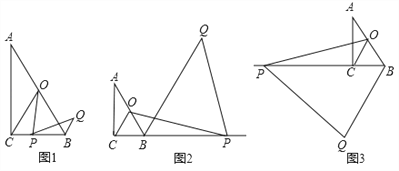
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)如图3,当点P在BC延长线上时,若∠BPO=15°,BP=4,请求出BQ的长.
相关试题

