【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,则AK= .
,则AK= . 
参考答案:
【答案】2 ![]() ﹣3
﹣3
【解析】解:连接BH,如图所示: 
∵四边形ABCD和四边形BEFG是正方形,
∴∠BAH=∠ABC=∠BEH=∠F=90°,
由旋转的性质得:AB=EB,∠CBE=30°,
∴∠ABE=60°,
在Rt△ABH和Rt△EBH中,![]() ,
,
∴Rt△ABH≌△Rt△EBH(HL),
∴∠ABH=∠EBH= ![]() ∠ABE=30°,AH=EH,
∠ABE=30°,AH=EH,
∴AH=ABtan∠ABH= ![]() ×
× ![]() =1,
=1,
∴EH=1,
∴FH= ![]() ﹣1,
﹣1,
在Rt△FKH中,∠FKH=30°,
∴KH=2FH=2( ![]() ﹣1),
﹣1),
∴AK=KH﹣AH=2( ![]() ﹣1)﹣1=2
﹣1)﹣1=2 ![]() ﹣3;
﹣3;
故答案为:2 ![]() ﹣3.
﹣3.
连接BH,由正方形的性质得出∠BAH=∠ABC=∠BEH=∠F=90°,由旋转的性质得:AB=EB,∠CBE=30°,得出∠ABE=60°,由HL证明Rt△ABH≌Rt△EBH,得出∠ABH=∠EBH= ![]() ∠ABE=30°,AH=EH,由三角函数求出AH,得出EH、FH,再求出KH=2FH,即可求出AK.
∠ABE=30°,AH=EH,由三角函数求出AH,得出EH、FH,再求出KH=2FH,即可求出AK.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.
ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8.(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是______________.位置关系是_______________.
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请做出判断并给与证明.


(图1) (图2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+5|+(b﹣4)2=0,则(a+b)2009= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形按边分类可分为( )
A. 不等边三角形、等边三角形
B. 等腰三角形、等边三角形
C. 不等边三角形、等腰三角形、等边三角形
D. 不等边三角形、等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形的底角的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周期间,欢欢一家随旅游团到某风景区旅游,集体门票的收费标准是:
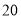 人以内(含
人以内(含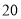 人),每人
人),每人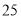 元;超过
元;超过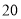 人的,超过的部分每人
人的,超过的部分每人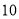 元.
元.(
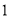 )写出应收门票费
)写出应收门票费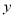 (元)与游览人数
(元)与游览人数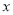 (人)(其中
(人)(其中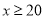 )之间的关系式.
)之间的关系式.(
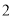 )利用(
)利用(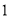 )中的关系式计算:若欢欢一家所在的旅游团共
)中的关系式计算:若欢欢一家所在的旅游团共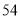 人,那么该旅游团购门票共花了多少钱?
人,那么该旅游团购门票共花了多少钱?
相关试题

