【题目】已知△ABC中,AC=BC,∠ACB=90゜,点P在射线AC上,连接PB,将线段PB绕点B逆时针旋转90゜得线段BN,AN交直线BC于M.
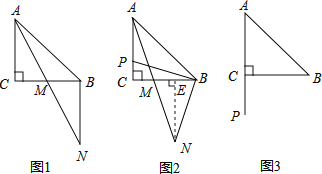
(1)如图1.若点P与点C重合,则![]() = ,
= ,![]() = (直接写出结果):
= (直接写出结果):
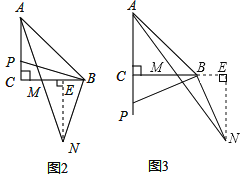
(2)如图2,若点P在线段AC上,求证:AP=2MC;
(3)如图3,若点P在线段AC的延长线上,完成图形,并直接写出![]() = .
= .
参考答案:
【答案】(1)1,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)先求出∠C=∠CBN,再利用“角角边”证明△ACM和△NBM全等,根据全等三角形对应边相等可得AM=MN,MC=MB,再求出AP=AC=2MC,然后求解即可;
(2)过点N作NE⊥BC于E,根据同角的余角相等求出∠PBC=∠BNE,然后利用“角角边”证明△PBC和△BNE全等,根据全等三角形对应边相等可得BE=PC,NE=BC,然后求出AP=CE,AC=NE,再利用“角角边”证明△ACM和△NEM全等根据全等三角形对应边相等可得MC=ME,整理即可得证;
(3)过点N作NE⊥BC交CB的延长线于E,然后与(2)的求解方法相同.
(1)解:∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠CBN=90°,BC=BN,
∴∠C=∠CBN,AC=BN,
在△ACM和△NBM中,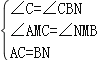 ,
,
∴△ACM≌△NBM(AAS),
∴AM=MN,MC=MB,
∴AP=AC=BC=MC+MB=2MC,
∴![]() =1,
=1,![]() =
=![]() ;
;
(2)证明:如图2,过点N作NE⊥BC于E,
∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,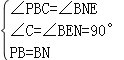 ,
,
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC﹣PC=BC﹣BE=CE,AC=NE,
在△ACM和△NEM中,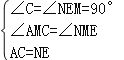 ,
,
∴△ACM≌△NEM(AAS),
∴MC=ME,
∴CE=2MC,
∴AP=2MC;
(3)解:如图3,过点N作NE⊥BC交CB的延长线于E,过点N作NE⊥BC于E,
∴∠BNE+∠CBN=90°,
∵线段PB绕点B逆时针旋转90゜得线段BN,
∴∠PBC+∠CBN=90°,
∴∠PBC=∠BNE,
在△PBC和△BNE中,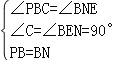 ,
,
∴△PBC≌△BNE(AAS),
∴BE=PC,NE=BC,
∴AP=AC﹣PC=BC﹣BE=CE,AC=NE,
在△ACM和△NEM中,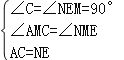 ,
,
∴△ACM≌△NEM(AAS),
∴MC=ME,
∵AP=AC+PC,
CE=BC+BE=2MC,
∴AP=CE=2MC,
∴![]() =
=![]() .
.
故答案为:(1)1,![]() ;(3)
;(3)![]() .
.
-
科目: 来源: 题型:
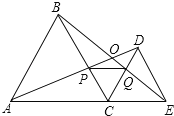
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
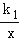 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).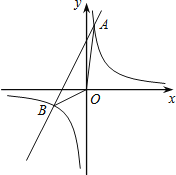
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=
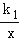 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一正数a的两个平方根分别是2m-3和5-m,求a的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc>0;②b2﹣4ac=0;③a>2;④方程ax2+bc+c=﹣2的根为x1=x2=﹣1;⑤若点B(﹣
 ,y1),C(﹣
,y1),C(﹣ ,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )
,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )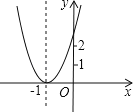
A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c经过A (1,0)、B(0,3)及C(3,0)点,动点D从原点O开始沿OB方向以每秒1个单位长度移动,动点E从点C开始沿CO方向以每秒1个长度单位移动,动点D、E同时出发,当动点E到达原点O时,点D、E停止运动.
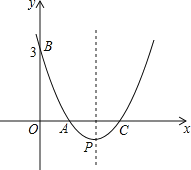
(1)求抛物线的解析式及顶点P的坐标;
(2)若F(﹣1,0),求△DEF的面积S与E点运动时间t的函数解析式;当t为何值时,△DEF的面积最大?最大面积是多少?
(3)当△DEF的面积最大时,抛物线的对称轴上是否存在一点N,使△EBN是直角三角形?若存在,求出N点的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
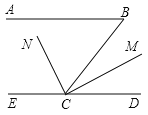
查看答案和解析>>【题目】如图,已知AB∥CD,∠B=50°,CM是∠BCD的平分线,CM⊥CN,求∠ECN的度数.
相关试题

