【题目】如图,在平面直角坐标系中,抛物线![]() 经过点A(﹣3,0)和点B(2,0).直线
经过点A(﹣3,0)和点B(2,0).直线![]() (
(![]() 为常数,且
为常数,且![]() )与BC交于点D,与
)与BC交于点D,与![]() 轴交于点E,与AC交于点F.
轴交于点E,与AC交于点F.
(1)求抛物线的解析式;
(2)连接AE,求![]() 为何值时,△AEF的面积最大;
为何值时,△AEF的面积最大;
(3)已知一定点M(﹣2,0).问:是否存在这样的直线![]() ,使△BDM是等腰三角形?若存在,请求出
,使△BDM是等腰三角形?若存在,请求出![]() 的值和点D的坐标;若不存在,请说明理由.
的值和点D的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在, ![]() ,D(
,D(![]() ,
,![]() ).
).
【解析】试题分析:(1)利用待定系数法即可解决问题.
(2)由题意可得点E的坐标为(0,h),点F的坐标为( ![]() ,h),根据S△AEF=
,h),根据S△AEF=![]() OEFE=
OEFE=![]() h
h![]() =-
=-![]() (h-3)2+
(h-3)2+![]() .利用二次函数的性质即可解决问题.
.利用二次函数的性质即可解决问题.
(3)分三种情形,分别列出方程即可解决问题.
试题解析:(1)将A(-3,0),点B(2,0)两点代入抛物线方程![]() 得,
得,
![]()
解得![]() ,
,
所以抛物线的解析式为![]() .
.
(2)如图所示,根据抛物线方程可知点C(0,6),
又∵A(-3,0)
∴直线AC的解析式为![]() ,
,
∵点F的纵坐标为![]() ,所以其横坐标为
,所以其横坐标为![]() ,即F(
,即F(![]() ,
,![]() )可得EF=
)可得EF=![]() ,
,
∴![]()
∴当![]() =3时,△AEF的最大面积为
=3时,△AEF的最大面积为![]() .
.
(3)∵B(2,0), C(0,6)
∴直线BC的解析式为![]() ,
,
∵点D的纵坐标为![]() ,所以其横坐标为
,所以其横坐标为![]() ,即D(
,即D(![]() ,
,![]() )
)
分三种情况讨论:
①当MD=BD时,点D应该在BM的垂直平分线y轴上,而![]() ﹤6∴点D不在y轴上,所以(舍)
﹤6∴点D不在y轴上,所以(舍)
②当MD=BM=4时,过D点做DQ⊥x轴于点Q, ∴MQ=![]() +2=4-
+2=4-![]() ,DQ=
,DQ= ![]()
在![]() 中
中![]() ∴
∴![]() 解得
解得![]() =0(舍)或
=0(舍)或![]() =
=![]()
∴D(![]() ,
,![]() )
)
③当BD=BM=4时,过D点做DQ⊥x轴于点Q, ∴BQ=2-![]() =
=![]() ,DQ=
,DQ= ![]()
在![]() 中
中![]() ∴
∴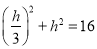 ,解得
,解得![]()
∴D(![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点
 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如下表:
第一次
第二次
第三次
第四次
第五次
第六次
第七次
第八次
第九次
第十次
甲
7
10
8
10
9
9
10
8
10
9
乙
10
7
10
9
9
10
8
10
7
10
(1)选手甲的成绩的中位数是__________分;选手乙的成绩的众数是__________分;
(2)计算选手甲的平均成绩和方差;
(2)已知选手乙的成绩的方差是1.4,则成绩较稳定的是哪位选手?(直按写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为奖励优秀学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元,购买2个文具袋和3个圆规需39元。
(1)求文具袋和圆规的单价。
(2)学校准备购买文具袋20个,圆规若干,文具店给出两种优惠方案:
方案一:购买一个文具袋还送1个圆规。
方案二:购买圆规10个以上时,超出10个的部分按原价的八折优惠,文具袋不打折.
①设购买面规m个,则选择方案一的总费用为______,选择方案二的总费用为______.
②若学校购买圆规100个,则选择哪种方案更合算?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b+2a=0;②abc>0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )个.
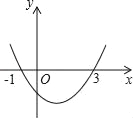
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在讲完乘法公式
 的多种运用后,要求同学们运用所学知识解答:求代数式
的多种运用后,要求同学们运用所学知识解答:求代数式 的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
的最小值?同学们经过交流、讨论,最后总结出如下解答方法:解:

∵
 ,
,当
 时,
时, 的值最小,最小值是0,
的值最小,最小值是0,∴

当
 时,
时, 的值最小,最小值是1,
的值最小,最小值是1,∴
 的最小值是1.
的最小值是1.请你根据上述方法,解答下列各题
(1)当x=______时,代数式
 的最小值是______;
的最小值是______;(2)若
 ,当x=______时,y有最______值(填“大”或“小”),这个值是______;
,当x=______时,y有最______值(填“大”或“小”),这个值是______;(3)若
 ,求
,求 的最小值.
的最小值.
相关试题

