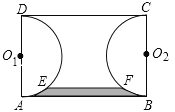
【题目】如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2,一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由![]() ,EF,
,EF,![]() ,AB所围成图形(图中阴影部分)的面积等于 .
,AB所围成图形(图中阴影部分)的面积等于 .
参考答案:
【答案】![]() ﹣
﹣![]() .
.
【解析】
试题解析:连接O1O2,O1E,O2F,则四边形O1O2FE是等腰梯形,过E作EG⊥O1O2,过F⊥O1O2,
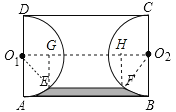
∴四边形EGHF是矩形,
∴GH=EF=2,
∴O1G=![]() ,
,
∵O1E=1,
∴GE=![]() ,
,
∴![]() ;
;
∴∠O1EG=30°,
∴∠AO1E=30°,
同理∠BO2F=30°,
∴阴影部分的面积=S矩形ABO2O1﹣2S扇形AO1E﹣S梯形EFO2O1=3×1﹣2×![]() =
=![]() (2+3)×
(2+3)×![]() =3﹣
=3﹣![]() ﹣
﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x+y=6, xy=7, 那么x2+y2=______,(x-y)2=__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2-4x+a是完全平方式,则a=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2007年4月18日开始,我国铁路第六次提速,某次列车平均提速v km/h.
(1)若提速前列车的平均速度为x km/h,行驶1200km的路程,提速后比提速前少用多长时间?
(2)若v=50,行驶1200km的路程,提速后所用时间是提速前的 ,求提速前列车的平均速度?
,求提速前列车的平均速度?
(3)用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50km,则提速前的平均速度为km/h. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE//OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2-12+36+|n-2m|=0.
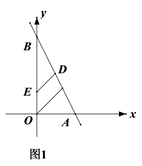
(1)求A、B两点的坐标?
(2)若点D为AB中点,求OE的长?
(3)如图2,若点P(x,-2x+6)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长分别为3和6,则这个三角形的周长是( )
A.15
B.12
C.12或15
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】等边三角形是轴对称图形,它的对称轴共有( )
A. 1条 B. 2 条 C. 3条 D. 无数条
相关试题

