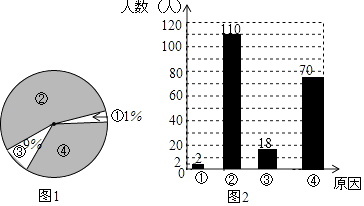
【题目】中国式过马路,是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关”针对这种现象某媒体记者在多个路口采访闯红灯的行人,得出形成这种现象的四个基本原因,①红绿灯设置不科学,交通管理混乱占1%;②侥幸心态;③执法力度不够占9%;④从众心理,该记者将这次调查情况整理并绘制了如下尚不完整的统计图,请根据相关信息,解答下列问题.
(1)该记者本次一共调査了名行人;
(2)求图1中④所在扇形的圆心角,并补全图2; 
(3)在本次调查中,记者随机采访其中的一名行人,求他属于第②种情况的概率.
参考答案:
【答案】
(1)200
(2)解:④所在扇形的圆心角 ![]() ×360°=126°,
×360°=126°,
③的人数200×9%=18人,②的人数200﹣18﹣2﹣70=110人,
第②种情况110人,第③种情况18,补全图形如图:
 .
.
(3)解:p= ![]() =
= ![]() ,
,
他属于第②种情况的概率为 ![]() .
.
【解析】解:(1)2÷1%=200(名). 故答案为200;
(1)根据①种的人数除以①所占的百分比,可得答案;(2)④种情况的人数除以总人数乘以360°,可得答案,总人数乘以第③种情况所占的百分比,可得第③种情况的人数,根据总人数减去第①种情况的人数,减去第③种情况的人数,减法第④种情况的人数,可得第②中情况的人数;
3)根据概率的意义:②的人数除以总人数,可得答案.
-
科目: 来源: 题型:
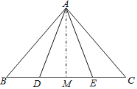
查看答案和解析>>【题目】已知点
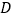 、
、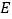 在
在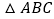 的
的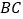 边上,
边上,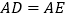 ,
,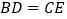 ,为了判断
,为了判断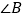 与
与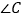 的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.
的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.解:作
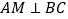 ,垂足为
,垂足为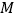
∵
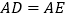 ,
,∴
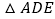 是________三角形,
是________三角形,∴
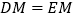 ________
________又∵
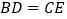 ,
,∴
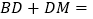 ________,即
________,即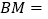 ________;
________;又∵________(自己所作),
∴
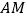 是线段________的垂直平分线;
是线段________的垂直平分线;∴
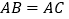 ________
________∴________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论: ①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )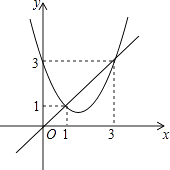
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式 12=1=
 ×1×2×(2+1)
×1×2×(2+1)
12+22= ×2×3×(4+1)
×2×3×(4+1)
12+22+32= ×3×4×(6+1)
×3×4×(6+1)
12+22+32+42= ×4×5×(8+1)…
×4×5×(8+1)…
可以推测12+22+32+…+n2= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=
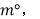 则∠BOE的度数是
则∠BOE的度数是
A.
 B.
B. 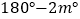 C.
C. 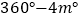 D.
D. 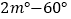
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级
 班数学课外兴趣小组在探究:“
班数学课外兴趣小组在探究:“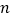 边形共有多少条对角线”这一问题时,设计了如下表格:
边形共有多少条对角线”这一问题时,设计了如下表格:多边形的边数
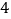
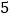
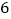
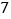
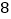
…
从多边形一个顶点出发可引起的对角线条数
…
多边形对角线的总条数
…
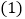 探究:假若你是该小组的成员,请把你研究的结果填入上表;
探究:假若你是该小组的成员,请把你研究的结果填入上表;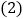 猜想:随着边数的增加,多边形对角线的条数会越来越多,从
猜想:随着边数的增加,多边形对角线的条数会越来越多,从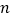 边形的一个顶点出发可引的对角线条数为多少,
边形的一个顶点出发可引的对角线条数为多少,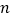 边形对角线的总条数为多少.
边形对角线的总条数为多少. 应用:
应用: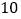 个人聚会,每不相邻的人都握一次手,共握多少次手?
个人聚会,每不相邻的人都握一次手,共握多少次手?
相关试题

