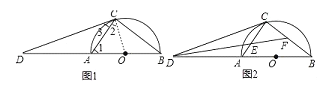
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,根据切线的性质、直径所对的圆周角是直角及等角的余角相等即可证明结论.
(2)①由∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,∠CDE=∠FDB,∠ECD=∠B,即可得∠CEF=∠CF,再由∠ECF=90°,可得∠CEF=∠CFE=45°,即可得结论.
②由勾股定理可求得AB=5,根据已知易证△DCA∽△DBC,得![]() ,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得
,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得![]() ,设EC=CF=x,列出方程即可解决问题.
,设EC=CF=x,列出方程即可解决问题.
试题解析:(1)证明:如图1中,连接OC.
∵OA=OC,
∴∠1=∠2,
∵CD是⊙O切线,
∴OC⊥CD,
∴∠DCO=90°,
∴∠3+∠2=90°,
∵AB是直径,
∴∠1+∠B=90°,
∴∠3=∠B.
(2)解:①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,
∵∠CDE=∠FDB,∠ECD=∠B,
∴∠CEF=∠CFE,∵∠ECF=90°,
∴∠CEF=∠CFE=45°,
∴tan∠CFE=tan45°=1.
②在RT△ABC中,∵AC=3,BC=4,
由勾股定理得AB=5,
∵∠CDA=∠BDC,∠DCA=∠B,
∴△DCA∽△DBC,
∴![]() ,设DC=3k,DB=4k,
,设DC=3k,DB=4k,
∵CD2=DADB,
∴9k2=(4k﹣5)4k,
∴k=![]() ,
,
∴CD=![]() ,DB=
,DB=![]() ,
,
∵∠CDE=∠BDF,∠DCE=∠B,
∴△DCE∽△DBF,
∴![]() ,设EC=CF=x,
,设EC=CF=x,
∴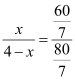 ,
,
∴x=![]() .
.
∴CE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列条件中能判断四边形是平行四边形的是().
A.对角线互相垂直
B.对角线相等
C.对角线互相垂直且相等
D.对角线互相平分 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个使四边形ABCD为平行四边形的选法有( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 △ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB=_____________.
△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB=_____________.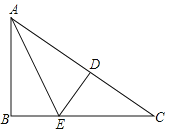
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,D,C,F在同一直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需添加一个条件是( )
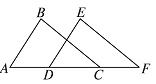
A. ∠BCA=∠F B. ∠B=∠E C. BC∥EF D. ∠A=∠EDF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+m(m>0)
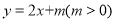 与x
与x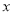 轴交于点A(-2,0)
轴交于点A(-2,0) 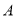 (
(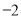 ,
,  ),直线
),直线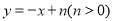 与
与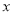 轴、
轴、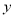 轴分别交于
轴分别交于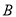 、
、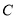 两点,并与直线
两点,并与直线 相交于点
相交于点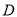 ,若
,若 .
.(1)求点
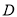 的坐标;
的坐标;(2)求出四边形
 的面积;
的面积;(3)若
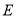 为
为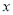 轴上一点,且
轴上一点,且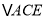 为等腰三角形,直接写出点
为等腰三角形,直接写出点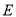 的坐标.
的坐标.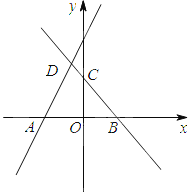
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值
(1)-(9x3-4x2+5)-(-3-8x3+3x2),其中x=-2;
(2)5xy﹣[x2+4xy﹣y2﹣(x2+2xy﹣2y2)]其中
 ,
,  .
.
相关试题

