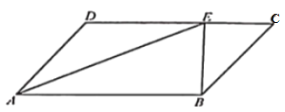
【题目】如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求证:∠BEC=90°;
(2)求cos∠DAE.
参考答案:
【答案】(1)见解析;(2)cos∠DAE=![]()
【解析】
(1)先求出BC的长,继而根据勾股定理的逆定理进行证明即可得;
(2)根据平行四边形的性质可求得AB=16,∠ABE=90°,继而根据勾股定理求出AE的长,然后利用余弦的定义求出cos∠EAB的值,再根据∠DAE=∠EAB即可求得答案.
(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC ,
∴∠AED=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠AED=∠DAE,
∴AD=DE=10,
∴BC=10,
又∵BE=8,CE=6,
∴BE2+CE2=BC2,
∴△BEC为直角三角形,
∴∠BEC=90°;
(2)∵ DE=10,CE=6,
∴CD=DE+CE=16,
∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD=16,
∴∠ABE=∠BEC=90°,
∴AE=![]() ,
,
∴cos∠EAB=![]() ,
,
∵∠DAE=∠EAB,
∴cos∠DAE==![]() .
.
-
科目: 来源: 题型:
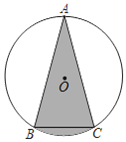
查看答案和解析>>【题目】如图,⊙O中,AB=AC,∠ACB=75°,BC=1,则阴影部分的面积是( )
A.1+
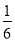 πB.
πB. πC.
πC.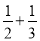 πD.1+
πD.1+ π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 A 的坐标是(﹣2,0),点 B 的坐标是(0,6),C 为 OB 的中点,将△ABC 绕点 B 逆时针旋转 90°后得到△A′B′C′.若反比例函数 y
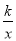 的图象恰好经过 A′B 的中点 D,则k _________.
的图象恰好经过 A′B 的中点 D,则k _________.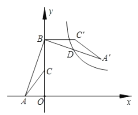
-
科目: 来源: 题型:
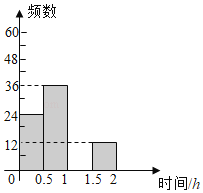
查看答案和解析>>【题目】扬州市“五个一百工程“在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如图不完整的频数分布表和频数分布直方图.
每天课外阅读时间t/h
频数
频率
0<t≤0.5
24
0.5<t≤1
36
0.3
1<t≤1.5
0.4
1.5<t≤2
12
b
合计
a
1
根据以上信息,回答下列问题:
(1)表中a= ,b= ;
(2)请补全频数分布直方图;
(3)若该校有学生1200人,试估计该校学生每天课外阅读时间超过1小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离
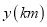 与小王的行驶时间
与小王的行驶时间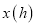 之间的函数关系.
之间的函数关系.请你根据图象进行探究:
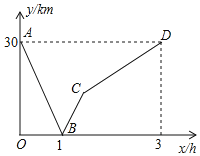
(1)小王和小李的速度分别是多少?
(2)求线段
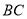 所表示的
所表示的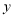 与
与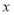 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量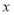 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
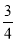 x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=
x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=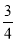 x2+bx+c经过点B,C,与x轴的另一个交点为点A.
x2+bx+c经过点B,C,与x轴的另一个交点为点A.(1)求抛物线的解析式;
(2)点P是直线BC下方的抛物线上一动点,求四边形ACPB的面积最大时点P的坐标;
(3)若点M是抛物线上一点,请直接写出使∠MBC=
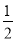 ∠ABC的点M的坐标.
∠ABC的点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线y1=﹣
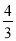 x与双曲线y=
x与双曲线y=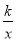 交于A,B两点,点C在x轴上,连接AC,BC.当AC⊥BC,S△ABC=15时,求k的值为( )
交于A,B两点,点C在x轴上,连接AC,BC.当AC⊥BC,S△ABC=15时,求k的值为( )
A.﹣10B.﹣9C.6D.4
相关试题

