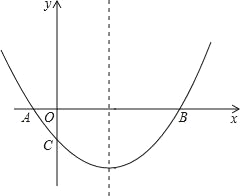
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0, ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ;(2)P(2,﹣
;(2)P(2,﹣![]() );(3)点N的坐标为(4,﹣
);(3)点N的坐标为(4,﹣![]() ),(2+
),(2+![]() ,
, ![]() )或(2﹣
)或(2﹣![]() ,
, ![]() ).
).
【解析】试题分析:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识,在解答(3)时要注意进行分类讨论.(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,![]() )三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(﹣1,0),B(5,0),C(0,![]() )三点在抛物线上,∴
)三点在抛物线上,∴ ,解得
,解得 .∴抛物线的解析式为:y=
.∴抛物线的解析式为:y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ;
;
(2)∵抛物线的解析式为:y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ,∴其对称轴为直线x=﹣
,∴其对称轴为直线x=﹣![]() =﹣
=﹣![]() =2,连接BC,如图1所示,
=2,连接BC,如图1所示,
∵B(5,0),C(0,﹣![]() ),∴设直线BC的解析式为y=kx+b(k≠0),∴
),∴设直线BC的解析式为y=kx+b(k≠0),∴ ,解得
,解得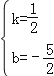 ,∴直线BC的解析式为y=
,∴直线BC的解析式为y=![]() x﹣
x﹣![]() ,当x=2时,y=1﹣
,当x=2时,y=1﹣![]() =﹣
=﹣![]() ,∴P(2,﹣
,∴P(2,﹣![]() );
);
(3)存在.如图2所示,
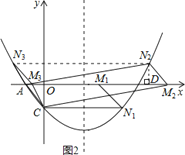
①当点N在x轴下方时,∵抛物线的对称轴为直线x=2,C(0,﹣![]() ),∴N1(4,﹣
),∴N1(4,﹣![]() );
);
②当点N在x轴上方时,如图2,过点N2作N2D⊥x轴于点D,在△AN2D与△M2CO中,
 ∴△AN2D≌△M2CO(ASA),∴N2D=OC=
∴△AN2D≌△M2CO(ASA),∴N2D=OC=![]() ,即N2点的纵坐标为
,即N2点的纵坐标为![]() .∴
.∴![]() x2﹣2x﹣
x2﹣2x﹣![]() =
=![]() ,
,
解得x=2+![]() 或x=2﹣
或x=2﹣![]() ,∴N2(2+
,∴N2(2+![]() ,
,![]() ),N3(2﹣
),N3(2﹣![]() ,
,![]() ).综上所述,符合条件的点N的坐标为N1(4,﹣
).综上所述,符合条件的点N的坐标为N1(4,﹣![]() ),N2(2+
),N2(2+![]() ,
,![]() )或N3(2﹣
)或N3(2﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
-
科目: 来源: 题型:
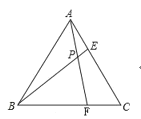
查看答案和解析>>【题目】如图,在边长为6的等边三角形ABC中,点E、F分别是边AC、BC上的动点,连接AF、BE,交于点P,若始终保持AE=CF,当点E从点A运动到点C时,则点P运动的路径长__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动阳光体育运动的广泛开展,引导学生积极参加体育锻炼,某校九年级准备购买一批运动鞋供学生借用,现从九年级各班随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:
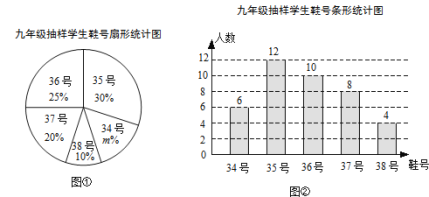
(1)接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)在本次调查中,学生鞋号的众数为 号,中位数为 号;
(3)根据样本数据,若该年级计划购买200双运动鞋,建议购买36号运动鞋多少双?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆内一点到圆周上的点的最大距离是7,最小距离是5,则该圆的半径是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M,以下结论:
①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=
 AF;⑤
AF;⑤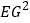 =FGDG,其中正确结论的个数为( )
=FGDG,其中正确结论的个数为( )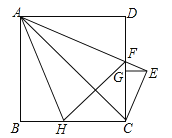
A. 2 B. 3 C. 4 D. 5
相关试题

